题目内容
棱长为2的正方体ABCD-A1B1C1D1的内切球的表面积为（ ）
A、
| ||
| B、16π | ||
| C、4π | ||
D、
|
分析：根据正方体和内切球半径之间的关系 即可求球的表面积．
解答：解：∵棱长为2的正方体ABCD-A1B1C1D1的内切球的直径等于正方体的棱长，
∴2r=2，即内切球的半径r=1，
∴内切球的表面积为4π．
故选：C．
∴2r=2，即内切球的半径r=1，
∴内切球的表面积为4π．
故选：C．
点评：本题主要考查球的表面积公式的计算，根据正方体的内切球和正方体棱长之间的关系是解决本题的关键．
练习册系列答案
相关题目
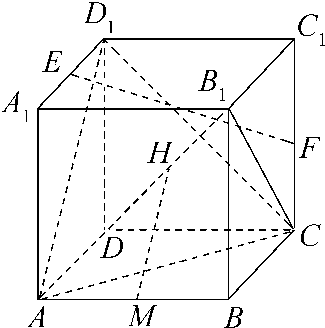如图，在棱长为2的正方体ABCD-A1B1C1D1中，E、F、M、H分别为A1D1、CC1、AB、DB1的中点．
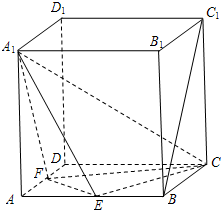（2007•静安区一模）（文）如图，在棱长为2的正方体ABCD-A1B1C1D1中，点E、F分别是棱AB、AD的中点．求：