题目内容
已知f(x)=ax3+bx2+cx+d(a≠0)是定义在R上的函数,其图象交x轴于A、B、C三点,若点B的坐标为(2,0)且f(x)在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.(1)求c的值;
(2)在函数f(x)的图象上,是否存在一点M(x0,y0),使得f(x)在点M的切线斜率为3b?若存在,求M的坐标;若不存在,说明理由;
(3)求|AC|的取值范围.
解:(1)∵f(x)在[-1,0]和[0,2]上有相反的单调性,
∴x=0是f(x)的一个极值点,故f′(0)=0,
即2ax2+2bx+c=0有一个解x=0,则c=0.
(2)∵f(x)交x轴于点B(2,0),∴8a+4b+d=0,即d=-4(b+2a).
令f′(x)=0,得2ax2+2bx=0,x1=0,x2=![]() .
.
∵f(x)在[0,2]和[4,5]上有相反的单调性,
∴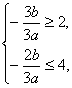 ∴-6≤
∴-6≤![]() ≤-3.
≤-3.
假设存在点M(x0,y0),使得f(x)在点M的切线斜率为3b,则f′(x0)=3b,
即3ax02+2bx0-3b=0.∵Δ=(2b)2-4×3a×(-3b)=4b2+36ab=4ab(![]() +9).
+9).
而-6≤![]() ≤-3,∴Δ<0.
≤-3,∴Δ<0.
故不存在点M(x0,y0),使得f(x)在点M的切线斜率为3b.
(3)设A(α,0),C(β,0),依题意可令
f(x)=α(x-α)(x-2)(x-β)=a[x3-(2+α+β)x2+(2α+2β+αβ)x-2αβ],
则![]() 即
即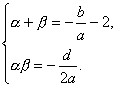
∴|AC|=|α-β|=![]() .
.
∵d=-4(b+2a),-6≤![]() ≤-3,
≤-3,
∴当![]() =-6时,|AC|max=43;当
=-6时,|AC|max=43;当![]() =-3时,|AC|min=3.
=-3时,|AC|min=3.
故3≤|AC|≤![]() .
.

| x2+1 |
| A、4 | B、0 | C、2m | D、-m+4 |
| b |
| x |
| f(a)-f(b) |
| a-b |
| A、恒小于0 | B、恒大于0 |
| C、可能为0 | D、可正可负 |