题目内容
已知F1,F2是双曲线的两个焦点,PQ是经过F1且垂直于实轴的弦,若△PQF2是等腰直角三角形,则双曲线的离心率为
1+
| 2 |
1+
.| 2 |
分析:设双曲线的方程为
-
=1,a>0,b>0,把x=-c代入双曲线的方程,得y=±
,由题设知2c=
,由此能求出双曲线的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
| b2 |
| a |
解答:解:设双曲线的方程为
-
=1,a>0,b>0,
∵F1,F2是双曲线的两个焦点,PQ是经过F1且垂直于实轴的弦,△PQF2是等腰直角三角形,
把x=-c代入双曲线的方程,得y=±
,
∴2c=
,即2ac=b2,
∴2ac=c2-a2,解得
=1+
,
=1-
(舍去),
∴双曲线的离心率为1+
.
故答案为:1+
.
| x2 |
| a2 |
| y2 |
| b2 |
∵F1,F2是双曲线的两个焦点,PQ是经过F1且垂直于实轴的弦,△PQF2是等腰直角三角形,
把x=-c代入双曲线的方程,得y=±
| b2 |
| a |
∴2c=
| b2 |
| a |
∴2ac=c2-a2,解得
| c |
| a |
| 2 |
| c |
| a |
| 2 |
∴双曲线的离心率为1+
| 2 |
故答案为:1+
| 2 |
点评:本题考查双曲线的离心率的求法,解题时要认真审题,合理取舍,注意合理地运用等价转化思想.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
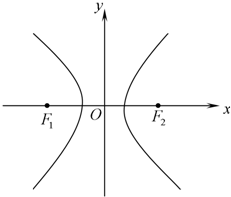
 的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.
的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.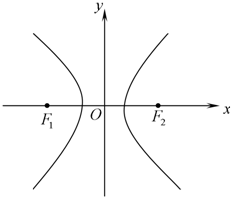
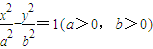 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若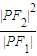 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )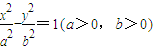 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若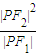 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )