题目内容
如图,在四边形 中,对角线
中,对角线 于
于 ,
, ,
,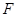 为
为 的重心,过点
的重心,过点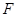 的直线
的直线 分别交
分别交 于
于 且
且 ‖
‖ ,沿
,沿 将
将 折起,沿
折起,沿 将
将 折起,
折起, 正好重合于
正好重合于 .
. 
(Ⅰ) 求证:平面 平面
平面 ;
;
(Ⅱ)求平面 与平面
与平面 夹角的大小.
夹角的大小.
(1)对于面面垂直的证明,主要是通过判定定理来分析得到,注意到 平面
平面 是解题的关键。
是解题的关键。
(2)
解析试题分析:解:(Ⅰ) 由题知:




 又
又
 平面
平面
 平面
平面
 平面
平面 平面
平面 6分
6分
(Ⅱ) 如图建立空间直角坐标系



 平面
平面
 平面
平面 的一个法向量为
的一个法向量为 8分
8分
又

设平面 的一个法向量为
的一个法向量为


取


 平面
平面 与平面
与平面 的夹角为
的夹角为 12分
12分
考点:空间中的面面位置关系
点评:对于空间中的垂直的证明主要是熟练的运用判定定理和性质定理来证明,同时二面角的求解,一般采用向量法来得到,属于基础题。

练习册系列答案
相关题目
 中,
中, 是棱
是棱 的中点.
的中点.
 平面
平面 ;
; .
. G是EF的中
G是EF的中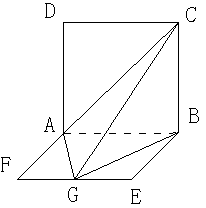
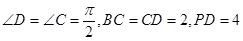 ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将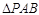 沿AB折到
沿AB折到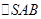 的位置,使
的位置,使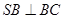 ,点E在SD上,且
,点E在SD上,且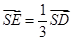 ,如下图。
,如下图。 平面ABCD;
平面ABCD;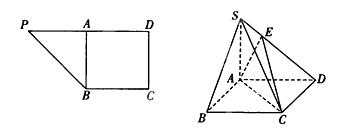
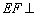 平面AEB,
平面AEB, ,
, ,
,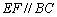 ,
,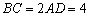 ,
,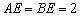 ,
, ,G是BC的中点.
,G是BC的中点.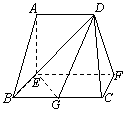
 ;
; 的大小.
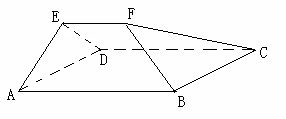
的大小. 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4, .
.
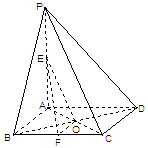
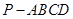 中,
中,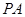 ⊥平面
⊥平面 ,
, 为
为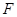 为
为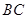 的中点,底面
的中点,底面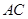 ,
, 交于点
交于点 .
.
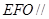 平面
平面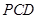 ;
; ⊥平面
⊥平面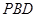 .
.
 ABC=60
ABC=60 ,EC
,EC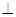 面ABCD,FA
面ABCD,FA