题目内容
函数f(x)= 单调递增区间是________.
单调递增区间是________.
[- +kπ,
+kπ,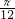 +kπ],(k∈Z)
+kπ],(k∈Z)
分析:根据两角差的余弦公式,将函数化简整理得f(x)=cos(2x- ),再结合余弦函数的单调性,解关于x的不等式即可得到函数f(x)的单调增区间.
),再结合余弦函数的单调性,解关于x的不等式即可得到函数f(x)的单调增区间.
解答:根据两角差的余弦公式,得
f(x)=
=cos[(2x+ )-
)- ]=cos(2x-
]=cos(2x- )
)
令-π+2kπ≤2x- ≤2kπ,(k∈Z)
≤2kπ,(k∈Z)
解之得,- +kπ≤x≤
+kπ≤x≤ +kπ,(k∈Z)
+kπ,(k∈Z)
∴函数的单调增区间为[- +kπ,
+kπ, +kπ],(k∈Z)
+kπ],(k∈Z)
故答案为:[- +kπ,
+kπ, +kπ],(k∈Z)
+kπ],(k∈Z)
点评:本题给出三角函数式,求函数的单调增区间,着重考查了两角差的余弦公式、余弦函数的单调性等知识,属于基础题.
 +kπ,
+kπ,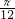 +kπ],(k∈Z)
+kπ],(k∈Z)分析:根据两角差的余弦公式,将函数化简整理得f(x)=cos(2x-
 ),再结合余弦函数的单调性,解关于x的不等式即可得到函数f(x)的单调增区间.
),再结合余弦函数的单调性,解关于x的不等式即可得到函数f(x)的单调增区间.解答:根据两角差的余弦公式,得
f(x)=

=cos[(2x+
 )-
)- ]=cos(2x-
]=cos(2x- )
)令-π+2kπ≤2x-
 ≤2kπ,(k∈Z)
≤2kπ,(k∈Z)解之得,-
 +kπ≤x≤
+kπ≤x≤ +kπ,(k∈Z)
+kπ,(k∈Z)∴函数的单调增区间为[-
 +kπ,
+kπ, +kπ],(k∈Z)
+kπ],(k∈Z)故答案为:[-
 +kπ,
+kπ, +kπ],(k∈Z)
+kπ],(k∈Z)点评:本题给出三角函数式,求函数的单调增区间,着重考查了两角差的余弦公式、余弦函数的单调性等知识,属于基础题.

练习册系列答案
相关题目
 ,则f(x)在(0,+∞)单调递 .
,则f(x)在(0,+∞)单调递 .