题目内容
设向量
=（-1，3，2），
=（4，-6，2），
=（-3，12，t），若=m+n，则t=________，m+n=________．
11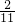 
分析：由向量的相等概念，若（a1，b1，c1）=（a2，b2，c2），则有a1=a2，且b1=b2，且c1=c2，从而可得含有m，n，t的方程组，求解m，n，t即可．
解答：m+n=（-m+4n，3m-6n，2m+2n），
∴（-m+4n，3m-6n，2m+2n）=（-3，12，t）．
∴
解得
∴
．
故答案为：11，．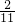
点评：本题考查空间向量的加法，向量的相等概念，向量的坐标运算．
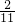
分析：由向量的相等概念，若（a1，b1，c1）=（a2，b2，c2），则有a1=a2，且b1=b2，且c1=c2，从而可得含有m，n，t的方程组，求解m，n，t即可．
解答：m
+n=（-m+4n，3m-6n，2m+2n），∴（-m+4n，3m-6n，2m+2n）=（-3，12，t）．
∴
解得∴
．故答案为：11，
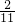．点评：本题考查空间向量的加法，向量的相等概念，向量的坐标运算．
练习册系列答案
黄冈冠军课课练系列答案
相关题目