题目内容
给出以下五个命题
①集合 与
与 都表示空集.
都表示空集.
② 是从
是从 到
到 的一个映射.
的一个映射.
③函数 是偶函数.
是偶函数.
④ 是定义在
是定义在 上的奇函数,则
上的奇函数,则
⑤ 是减函数.
是减函数.
以上命题正确的序号为:
② ④
解析试题分析:①集合 与
与 都表示空集,不对,因为,
都表示空集,不对,因为, 中有元素
中有元素 ,不是空集;
,不是空集;
② 是从
是从 到
到 的一个映射,正确,因为,对
的一个映射,正确,因为,对 中任意一个元素,按
中任意一个元素,按 ,在
,在 中都有唯一一个元素与之对应;
中都有唯一一个元素与之对应;
③函数 是偶函数,不正确,定义域不关于原点对称;
是偶函数,不正确,定义域不关于原点对称;
④ 是定义在
是定义在 上的奇函数,则
上的奇函数,则 ,正确,因为,
,正确,因为, ,
, ;
;
⑤ 是减函数,不对,只能说其在区间
是减函数,不对,只能说其在区间 是减函数。故答案为② ④。
是减函数。故答案为② ④。
考点:集合,映射,函数的奇偶性、单调性。
点评:简单题,本题通过判断几个命题的真假,较全面的考查集合,映射,函数的奇偶性、单调性。难度不大,关键看基础知识的掌握情况。

练习册系列答案
相关题目
 ¢.
¢.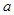 的取值范围是 ;
的取值范围是 ; 时,若
时,若 ,则
,则 的最大值是 .
的最大值是 . ,则
,则 = .
= . ,
, ,
,  ,若
,若 ,则实数
,则实数 的取值范围是____________.
的取值范围是____________.  ,
, ,则
,则 .
. 
 且
且 ,则实数a的取值范围是---。
,则实数a的取值范围是---。  是(0,+∞)上的增函数},
是(0,+∞)上的增函数}, ,则
,则 ;
; |
| 且
且 }中的元素按上小下大,左小右大的顺序排成如图的三角形数表,将数表中位于第
}中的元素按上小下大,左小右大的顺序排成如图的三角形数表,将数表中位于第 行第
行第 列的数记为
列的数记为 (
( ),则
),则 = .
= .
 ,集合
,集合 ,则集合
,则集合 .
.