题目内容
现有8名奥运会志愿者,其中志愿者 通晓日语,
通晓日语,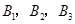 通晓俄语,
通晓俄语, 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(Ⅰ)求 被选中的概率;
被选中的概率;
(Ⅱ)求 和
和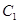 不全被选中的概率.
不全被选中的概率.
 通晓日语,
通晓日语,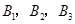 通晓俄语,
通晓俄语, 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.(Ⅰ)求
 被选中的概率;
被选中的概率; (Ⅱ)求
 和
和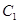 不全被选中的概率.
不全被选中的概率.(Ⅰ) .(Ⅱ)
.(Ⅱ) .
.
 .(Ⅱ)
.(Ⅱ) .
.(1)先求出从8人中选出日语、俄语和韩语志愿者各1名,其一切可能的结果组成的基本事件空间有18个基本事件.然后再求出“ 恰被选中”这一事件包含6个基本事件,所以所求事件的概率为
恰被选中”这一事件包含6个基本事件,所以所求事件的概率为 .
.
(2) 本小题易采用对立事件求解.用 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件.
全被选中”这一事件.
解:(Ⅰ)从8人中选出日语、俄语和韩语志愿者各1名,其一切可能的结果组成的基本事件空间 {
{ ,
, ,
,
 ,
, ,
, ,
,
 ,
, ,
, ,
,

 } 3分
} 3分
由18个基本事件组成.由于每一个基本事件被抽取的机会均等,因此这些基本事件的发生是等可能的.用 表示“
表示“ 恰被选中”这一事件,则
恰被选中”这一事件,则
 {
{ ,
,

 } 5分
} 5分
事件 由6个基本事件组成,
由6个基本事件组成,
 因而
因而 . 7分
. 7分
(Ⅱ)用 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件,
全被选中”这一事件,
由于 {
{ },事件
},事件 有3个基本事件组成,
有3个基本事件组成,
所以 ,由对立事件的概率公式得
,由对立事件的概率公式得 .……12分
.……12分
 恰被选中”这一事件包含6个基本事件,所以所求事件的概率为
恰被选中”这一事件包含6个基本事件,所以所求事件的概率为 .
.(2) 本小题易采用对立事件求解.用
 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件.
全被选中”这一事件.解:(Ⅰ)从8人中选出日语、俄语和韩语志愿者各1名,其一切可能的结果组成的基本事件空间
 {
{ ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 } 3分
} 3分由18个基本事件组成.由于每一个基本事件被抽取的机会均等,因此这些基本事件的发生是等可能的.用
 表示“
表示“ 恰被选中”这一事件,则
恰被选中”这一事件,则 {
{ ,
,
 } 5分
} 5分事件
 由6个基本事件组成,
由6个基本事件组成, 因而
因而 . 7分
. 7分 (Ⅱ)用
 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件,
全被选中”这一事件,由于
 {
{ },事件
},事件 有3个基本事件组成,
有3个基本事件组成,所以
 ,由对立事件的概率公式得
,由对立事件的概率公式得 .……12分
.……12分
练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
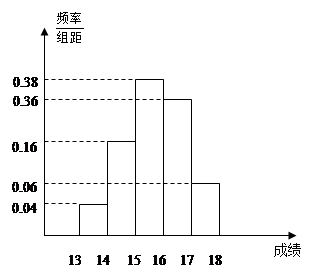
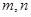 表示该班两位同学百米测试成绩且
表示该班两位同学百米测试成绩且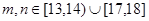 ,求
,求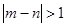 的概率
的概率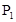 ,乙通过测试的概率为
,乙通过测试的概率为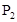 ,则甲、乙至少1人通过测试的概率为( )
,则甲、乙至少1人通过测试的概率为( )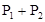
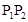
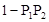
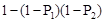
 ,则事件A恰好发生一次的概率为( )
,则事件A恰好发生一次的概率为( )



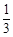 和
和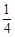 ,求(1)恰有1人译出密码的概率;
,求(1)恰有1人译出密码的概率;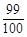 ,至少需要多少个乙这样的人?
,至少需要多少个乙这样的人?
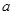 ,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为
,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为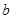 .求关于
.求关于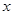 的一元二次方程
的一元二次方程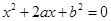 有实根的概率;
有实根的概率; 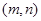 作为点P的坐标,求点P落在区域
作为点P的坐标,求点P落在区域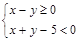 内的概率.
内的概率.



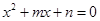 中,m,n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( )
中,m,n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( )


