题目内容
13. 如图,在四棱锥P-ABCD中,底面ABCD是正方形.已知AP=PB=AD=2,PD=2$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是正方形.已知AP=PB=AD=2,PD=2$\sqrt{2}$.(Ⅰ)求证:AD⊥PB;
(Ⅱ)求四棱锥P-ABCD的体积V;
(Ⅲ)设PC与平面ABCD所成角的大小为θ,求tanθ的值.
分析 (Ⅰ)由已知推导出AD⊥AB,AD⊥PA,由此能证明AD⊥平面PAB,从而得到AD⊥PB.
(Ⅱ)取AB的中点E,连接PE,CE,由已知推导出$PE⊥AB,PE=\sqrt{3}$,PE是四棱锥P-ABCD的高,由此能求出四棱锥P-ABCD的体积.
(Ⅲ)由PE⊥平面ABCD,得∠PCE即为PC与平面ABCD所成的角,由此能求出tanθ的值.
解答  (Ⅰ)证明:∵在四棱锥P-ABCD中底面ABCD是矩形,
(Ⅰ)证明:∵在四棱锥P-ABCD中底面ABCD是矩形,
∴AD⊥AB,
∵AD=PA=2,$PD=2\sqrt{2}$,
∴AD⊥PA,…(1分)
又∵AB∩PA=A,∴AD⊥平面PAB…(3分)
∵PB?平面PAB,∴AD⊥PB.…(4分)
(Ⅱ)解:取AB的中点E,连接PE,CE,
∵PA=PB=AB=2,∴$PE⊥AB,PE=\sqrt{3}$,…(6分)
∵AD⊥平面PAB,AD⊆平面ABCD,
∴平面PAB⊥平面ABCD,∴PE⊥平面ABCD,
∴PE是四棱锥P-ABCD的高,…(8分)
∴四棱锥P-ABCD的体积$V=\frac{1}{3}×2×2×\sqrt{3}=\frac{{4\sqrt{3}}}{3}$.…(9分)
(Ⅲ)解:∵PE⊥平面ABCD,
∴∠PCE即为PC与平面ABCD所成的角,…(10分)
∵$CE=\sqrt{B{C^2}+B{E^2}}=\sqrt{5}$…(11分)
∴$tanθ=\frac{PE}{CE}=\frac{{\sqrt{3}}}{{\sqrt{5}}}=\frac{{\sqrt{15}}}{5}$.…(13分)
点评 本题考查异面直线垂直的证明,考查四棱锥的体积的求法,考查角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 在侧面ABB1A1为长方形的三棱柱ABC-A1B1C1中,AB=a,AA1=$\sqrt{2}$a,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,且OC=OA.
在侧面ABB1A1为长方形的三棱柱ABC-A1B1C1中,AB=a,AA1=$\sqrt{2}$a,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,且OC=OA.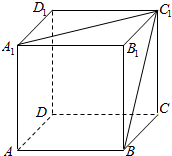 在正方体ABCD-A1B1C1D1中,求:
在正方体ABCD-A1B1C1D1中,求: 如图,在五面体ABCDEF中,四边形ABCD是边长为4的正方形,EF∥AD,
如图,在五面体ABCDEF中,四边形ABCD是边长为4的正方形,EF∥AD, 在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠BAD=60°,AE⊥BD.
在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠BAD=60°,AE⊥BD.