题目内容
已知数列{an},{bn}中,对任何正整数n都有: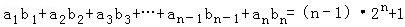 .
.
(1)若数列{bn}是首项为1和公比为2的等比数列,求数列{an}的通项公式;
(2)求证: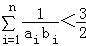 .
.
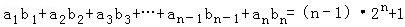 .
.(1)若数列{bn}是首项为1和公比为2的等比数列,求数列{an}的通项公式;
(2)求证:
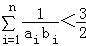 .
.解:(1)依题意,数列{bn}的通项公式为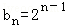 ,由
,由 ,
,
可得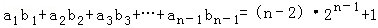 (n≥2),
(n≥2),
两式相减可得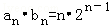 ,即an=n.
,即an=n.
当n=1时,a1=1,从而对一切n∈N*,都有an=n.
所以数列{an}的通项公式是an=n.
(2)证明:由(1)知,anbn=n·2n﹣1,
故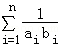 =
= +
+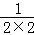 +
+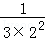 +…+
+…+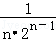 <
<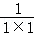 +
+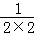 +
+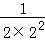 +…+
+…+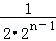 (n≥3).
(n≥3).
∴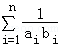 <
< +
+ +
+ +…+
+…+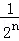 =1+
=1+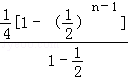 =1+
=1+ ﹣
﹣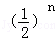 <
< .
.
即 成立.
成立.
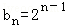 ,由
,由 ,
,可得
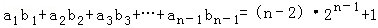 (n≥2),
(n≥2),两式相减可得
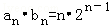 ,即an=n.
,即an=n.当n=1时,a1=1,从而对一切n∈N*,都有an=n.
所以数列{an}的通项公式是an=n.
(2)证明:由(1)知,anbn=n·2n﹣1,
故
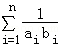 =
= +
+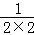 +
+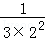 +…+
+…+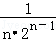 <
<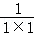 +
+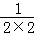 +
+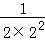 +…+
+…+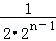 (n≥3).
(n≥3).∴
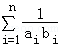 <
< +
+ +
+ +…+
+…+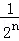 =1+
=1+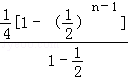 =1+
=1+ ﹣
﹣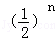 <
< .
.即
 成立.
成立.
练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目