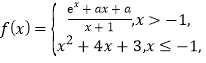题目内容
【题目】已知函数
，
，若方程
在
有四个不同的解，则
的取值范围为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
因为函数
，
都是偶函数，所以方程
在
有四个不同的解，只需在
上，
的图象两个不同的交点，画出函数图象，求出两函数图象相切时的
值，利用数形结合可得结果.
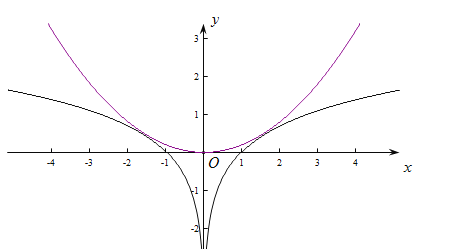
因为函数，都是偶函数，
所以方程在有四个不同的解，
只需在上，的图象在两个不同的交点，
不合题意，
当
时，
,当
，
即交点横坐标在上，
假定两函数的图象在点
处相切，
即两函数的图象在点处有相同的切线，
则有
，则有
，解得
，
则有
，
可得
，则有
，解得
，
因为越小开口越大，
所以要使得
，
在上，恰有两个不同的交点，
则
的取值范围为
，
此时，
的图象在
四个不同的交点，
方程在有四个不同的解，
所以的取值范围是，故选A.
练习册系列答案
阅读快车系列答案
相关题目
