题目内容
若直线x-y-2=0被圆(x-a)2+y2=4所截得的弦长为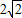 ,则实数a的值为 .
,则实数a的值为 .
【答案】分析:由圆的方程,得到圆心与半径,再求得圆心到直线的距离,由 求解.
求解.
解答:解:∵圆(x-a)2+y2=4
∴圆心为:(a,0),半径为:2
圆心到直线的距离为:
∵ ,
,
即 ,
,
∴a=4,或a=0.
故答案为:0或4.
点评:本题考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,得到 ,这是解题的关键.
,这是解题的关键.
 求解.
求解.解答:解:∵圆(x-a)2+y2=4
∴圆心为:(a,0),半径为:2
圆心到直线的距离为:

∵
 ,
,即
 ,
,∴a=4,或a=0.
故答案为:0或4.
点评:本题考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,得到
 ,这是解题的关键.
,这是解题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则实数a的值为________.
,则实数a的值为________.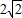 ,则实数a的值为 .
,则实数a的值为 .