Question

【题目】已知函数， .

（1）求的单调区间；

（2）若图像上任意一点处的切线的斜率，求的取值范围；

（3）若对于区间上任意两个不相等的实数都有成立，求的取值范围.

Answer 1

【答案】（1）见解析；（2）；（3）

【解析】试题分析：

（1）求导数后，解不等式可得函数的单调区间．（2）由题意可求得导函数的最小值为，可得，结合，可得，即为所求范围．（3）由题意得当时， 在区间上恒单调递减，故有．然后根据的取值的到函数的单调性，从而去掉中的绝对值，将问题转化为函数在区间上单调的问题处理，结合导函数的符号可求得所求范围．

试题解析：

（1）由，

得

因为,

所以由得；

由得．

所以函数的单调递增区间为，单调递减区间为．

（2）由（1）可知，

所以，

由，得，

整理得，

解得

又，

所以．

故实数的取值范围为．

（3）不妨设，

当时， 在区间上恒单调递减，有

①当时， 在区间上单调递减，

故，

则等价于，

令，由知在区间上单调递减，

又，

所以当时， 恒成立，

所以，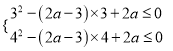

解得．

② ．

③当， 在区间上单调递增，

故

则等价于，

令，由知在区间上单调递减，

又，

所以当时， 恒成立，

所以，

解得，

综上可得实数的取值范围为．