题目内容
如图，在杨辉三角中，斜线l的上方，从1开始箭头所示的数组成一个锯齿形数列：1，3，3，4，6，5，10，…，记其n项和为Sn，则S21等于
- A.229
- B.283
- C.361
- D.374
C
分析：由图中锯齿形数列排列，发现规律：奇数项的第n项可以表示成正整数的前n项和的形式，偶数项构成以3为首项，公差是1的等差数列．由此再结合等差数列的通项与求和公式，即可得到S21的值．
解答：根据图中锯齿形数列的排列，发现
a1=1，a3=3=1+2，a5=6=1+2+3，…a21=1+2+3+…+11
而a2=3，a4=4，a6=5，…，a20=12
∴前21项的和S21=[1+（1+2）+（1+2+3）+…+（1+2+…+11）]+（3+4+5+…+12）=（1×11+2×10+3×9+…+10×2+11）+
因此，S21=286+75=361
故选C
点评：本题以杨辉三角为例，求锯齿形数列的前n项和，着重考查了等差数列的通项与求和公式和归纳推理的一般方法等知识点，属于基础题．
分析：由图中锯齿形数列排列，发现规律：奇数项的第n项可以表示成正整数的前n项和的形式，偶数项构成以3为首项，公差是1的等差数列．由此再结合等差数列的通项与求和公式，即可得到S21的值．
解答：根据图中锯齿形数列的排列，发现
a1=1，a3=3=1+2，a5=6=1+2+3，…a21=1+2+3+…+11
而a2=3，a4=4，a6=5，…，a20=12
∴前21项的和S21=[1+（1+2）+（1+2+3）+…+（1+2+…+11）]+（3+4+5+…+12）=（1×11+2×10+3×9+…+10×2+11）+
因此，S21=286+75=361
故选C
点评：本题以杨辉三角为例，求锯齿形数列的前n项和，着重考查了等差数列的通项与求和公式和归纳推理的一般方法等知识点，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图，在杨辉三角中，从上往下数共有n（n∈N*）行，在这些数中非1的数字之和是
如图，在杨辉三角中（三角形两腰数字为1，其余各项等于两肩数字之和），从上往下共有n行，则这些数中不是1的数字之和为（ ）| A、2n-2n | B、2n-2n+1 | C、2n-1 | D、n2-2n+1 |
如图，在杨辉三角中，斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}：1，3，3，4，6，5，10，…，记其前n项和为Sn，则S21的值为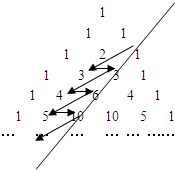
如图，在杨辉三角中，斜线l的上方，从1开始箭头所示的数组成一个锯齿形数列：1，3，3，4，6，5，10，…，记其n项和为Sn，则S21等于（ ）
如图，在杨辉三角中，斜线上方的数组成数列：1，3，6，10，…，记这个数列的前n项和为Sn，则