题目内容
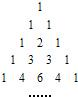如图，在杨辉三角中，从上往下数共有n（n∈N*）行，在这些数中非1的数字之和是分析：观察可知，第n（n∈N*）行中有n个数，从左向右依次是二项式系数Cn-10，Cn-11，Cn-12，Cn-1n-1，故当n≥3时，第n行各数的和为an=Cn-11+Cn-12+…+Cn-1n-2=2n-1-2．由此可知前n行非1的数字之和为a3+a4+…+an=
-2（n-2）=2n-2n．
| 4(1-2n-2) |
| 1-2 |
解答：解：观察可知，第n（n∈N*）行中有n个数，
从左向右依次是二项式系数Cn-10，Cn-11，Cn-12，Cn-1n-1，
故当n≥3时，除了1外，第n行各数的和为an=Cn-11+Cn-12+…+Cn-1n-2=2n-1-2．
又前两行全部为数字1，
故前n行非1的数字之和为a3+a4+…+an=
-2（n-2）=2n-2n．
答案：2n-2n
从左向右依次是二项式系数Cn-10，Cn-11，Cn-12，Cn-1n-1，
故当n≥3时，除了1外，第n行各数的和为an=Cn-11+Cn-12+…+Cn-1n-2=2n-1-2．
又前两行全部为数字1，
故前n行非1的数字之和为a3+a4+…+an=
| 4(1-2n-2) |
| 1-2 |
答案：2n-2n
点评：本题考查数列的性质和应用，解题时要注意观察能力和分析能力的培养．
练习册系列答案
相关题目
如图，在杨辉三角中（三角形两腰数字为1，其余各项等于两肩数字之和），从上往下共有n行，则这些数中不是1的数字之和为（ ）| A、2n-2n | B、2n-2n+1 | C、2n-1 | D、n2-2n+1 |
如图，在杨辉三角中，斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}：1，3，3，4，6，5，10，…，记其前n项和为Sn，则S21的值为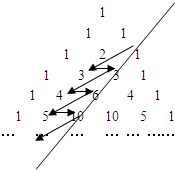
如图，在杨辉三角中，斜线l的上方，从1开始箭头所示的数组成一个锯齿形数列：1，3，3，4，6，5，10，…，记其n项和为Sn，则S21等于（ ）
如图，在杨辉三角中，斜线上方的数组成数列：1，3，6，10，…，记这个数列的前n项和为Sn，则