题目内容
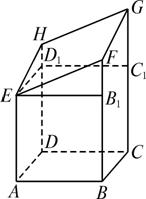
ABCD—EFGH表示以AB=4 cm,BC=3 cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面,当AE=5 cm,BF=8 cm,CG=12 cm时,试回答下列问题:(1)求DH的长;
(2)求这个几何体的体积;
(3)截面四边形EFGH是什么图形?并证明你的结论.
解析:(1)过E作EB1⊥BF,由BB1=AE=5,所以B1F=8-5=3.
∵平面ABEF∥平面DCGH,EF和HG是它们分别与截面的交线,
∴EF∥HG.
过H作HC1⊥CG,垂足为C1,则
GC1=FB1=3 cm,
DH=12-3=9 cm.
(2)用一个与该几何体完全相同的几何体,倒置其上,使它们拼接组合成一个以ABCD为底,高为17 cm的长方体,设原几何体的体积为V,则
2V=3×4×17=204 cm3,即V=102 cm3.
(3)已知EF∥HG,同理EH∥FG,于是EFGH是平行四边形.
∵![]() ,过E作ED1⊥DH,
,过E作ED1⊥DH,
则DD1=AE=5,ED1=AD=3,HD1=9-5=4,
∴![]() .
.
∴EF=EH,故EFGH是菱形.

(08年新建二中六模文)有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一组成.
第一排 | 明文字符 | A | B | C | D |
密码字符 | 11 | 12 | 13 | 14 | |
第二排 | 明文字符 | E | F | G | H |
密码字符 | 21 | 22 | 23 | 24 | |
第三排 | 明文字符 | M | N | P | Q |
密码字符 | 1 | 2 | 3 | 4 |
(Ⅰ)求密码中有两个不同数字的概率。
(Ⅱ)求密码中有三个不同数字的概率。
(08年新建二中六模理)有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一组成.
第一排 | 明文字符 | A | B | C | D |
密码字符 | 11 | 12 | 13 | 14 | |
第二排 | 明文字符 | E | F | G | H |
密码字符 | 21 | 22 | 23 | 24 | |
第三排 | 明文字符 | M | N | P | Q |
密码字符 | 1 | 2 | 3 | 4 |
设随机变量ξ表示密码中不同数字的个数.
(Ⅰ)求P(ξ=2)
(Ⅱ)求随机变量ξ的分布列和它的数学期望.
有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表,明文由表中每一排取一个字符组成且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同次序排列组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
(Ⅰ)求P(ξ=2);
(Ⅱ)求ξ的概率分布列和它的数学期望.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
(Ⅰ)求P(ξ=2);
(Ⅱ)求ξ的概率分布列和它的数学期望.