题目内容

设以向量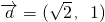 $数学公式$ 为方向向量的直线与椭圆 $数学公式$ 交于不同的两点P、Q．若点P、Q在x轴上的射影恰好为椭圆的两个焦点，则该椭圆的离心率为________．

$\text{[math]}$
分析：确定两个交点坐标，代入椭圆方程，化简可得结论．
解答：由题意，两个交点横坐标是-c，c，所以两个交点分别为（-c，- $\text{[math]}$ ），（c， $\text{[math]}$ ）
代入椭圆方程可得 $\text{[math]}$ ，两边乘2a²b²
∴c²（2b²+a²）=2a²b²
∵b²=a²-c²
∴c²（3a²-2c²）=2a⁴-2a²c²
∴2a⁴-5a²c²+2c⁴=0
∴（2a²-c²）（a²-2c²）=0
∴ $\text{[math]}$ =2，或 $\text{[math]}$ = $\text{[math]}$
∵0＜e＜1
∴e= $\text{[math]}$ = $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题主要考查了椭圆的简单性质，解题的关键是确定椭圆方程中a，b和c的关系．

练习册系列答案

黄冈经典阅读系列答案

文言文课外阅读特训系列答案

轻松阅读训练系列答案

南大教辅初中英语任务型阅读与首字母填空系列答案

初中英语听力与阅读系列答案

领航英语阅读理解与完形填空系列答案

英语拓展听力与阅读系列答案

阅读组合突破系列答案

初中英语阅读系列答案

全程探究阅读系列答案

相关题目

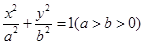若椭圆的左、右焦点分别为F₁，F₂，椭圆的离心率为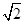：2．（1）过点C（-1,0）且以向量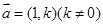为方向向量的直线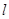交椭圆于不同两点A、B，若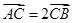，则当△OAB的面积最大时，求椭圆的方程。

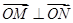（2）设M，N为椭圆上的两个动点，，过原点O作直线MN的垂线OD，垂足为D，求点D的轨迹方程．

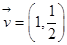已知以向量为方向向量的直线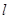过点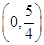，抛物线C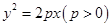：的顶点关于直线的对称点在该抛物线的准线上．

（Ⅰ）求抛物线C的方程；

（Ⅱ）设A、B是抛物线C上两个动点，过A作平行于x轴的直线m，直线OB与直线m交于点N，若 (O为原点，A、B异于原点)，试求点N的轨迹方程．

已知以向量

为方向向量的直线l过点

，抛物线C：y²=2px（p＞0）的顶点关于直线l的对称点在该抛物线的准线上．
（Ⅰ）求抛物线C的方程；
（Ⅱ）设A、B是抛物线C上两个动点，过A作平行于x轴的直线m，直线OB与直线m交于点N，若

（O为原点，A、B异于原点），试求点N的轨迹方程．

已知以向量

为方向向量的直线l过点

，抛物线C：y²=2px（p＞0）的顶点关于直线l的对称点在该抛物线的准线上．
（Ⅰ）求抛物线C的方程；
（Ⅱ）设A、B是抛物线C上两个动点，过A作平行于x轴的直线m，直线OB与直线m交于点N，若

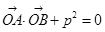（O为原点，A、B异于原点），试求点N的轨迹方程．