题目内容
甲、乙两条流水线包装同一种产品,在自动包装传送带上每隔30分钟抽取一包产品,称其重量,分别记录抽查数据如下:
甲:52、51、49、48、54、48、49、49
乙:60、63、40、45、46、58、43、45
(I)画出这两组数据的茎叶图,并求出甲组数据的方差;
(II)从甲中任取一个数据x(x≥50),从乙中任取一个数据y(y≤50),求满足|x-y|≤10的概率.
甲:52、51、49、48、54、48、49、49
乙:60、63、40、45、46、58、43、45
(I)画出这两组数据的茎叶图,并求出甲组数据的方差;
(II)从甲中任取一个数据x(x≥50),从乙中任取一个数据y(y≤50),求满足|x-y|≤10的概率.
分析:(Ⅰ)根据题意,由题干中数据可得茎叶图,由甲的数据,先计算甲的平均数,进而由方差公式,计算可得答案;
(Ⅱ)用(x,y)表示抽取的结果,根据题意,列举可得(x,y)的全部情况,分析可得|x-y|≤10的情况数目,由等可能事件的概率公式,计算可得答案.
(Ⅱ)用(x,y)表示抽取的结果,根据题意,列举可得(x,y)的全部情况,分析可得|x-y|≤10的情况数目,由等可能事件的概率公式,计算可得答案.
解答: 解:(Ⅰ)根据题意,由抽查数据可以作茎叶图如右,
解:(Ⅰ)根据题意,由抽查数据可以作茎叶图如右,
对于甲,其平均数
=
(52+51+49+48+54+48+49+49)=50,
其方差S2=
[(52-50)+(51-50)+(49-50)+(48-50)+(54-50)+(48-50)+(49-50)+(49-50)]=4,
(Ⅱ)用(x,y)表示抽取的结果,
则(x,y)有(54,40)、(54,43)、(54,45)、(54,45)、(54,46)、
(52,40)、(52,43)、(52,45)、(52,45)、(52,46)、
(51,40)、(51,43)、(51,45)、(51,45)、(51,46),共15种情况,
其中满足|x-y|≤10的有(54,45)、(54,45)、(54,46)、(52,43)、(52,45)、(52,45)、(52,46)、(51,43)、(51,45)、(51,45)、(51,46),共11种情况,
则|x-y|≤10的概率为
.
 解:(Ⅰ)根据题意,由抽查数据可以作茎叶图如右,
解:(Ⅰ)根据题意,由抽查数据可以作茎叶图如右,对于甲,其平均数
. |
| X |
| 1 |
| 8 |
其方差S2=
| 1 |
| 8 |
(Ⅱ)用(x,y)表示抽取的结果,
则(x,y)有(54,40)、(54,43)、(54,45)、(54,45)、(54,46)、
(52,40)、(52,43)、(52,45)、(52,45)、(52,46)、
(51,40)、(51,43)、(51,45)、(51,45)、(51,46),共15种情况,
其中满足|x-y|≤10的有(54,45)、(54,45)、(54,46)、(52,43)、(52,45)、(52,45)、(52,46)、(51,43)、(51,45)、(51,45)、(51,46),共11种情况,
则|x-y|≤10的概率为
| 11 |
| 15 |
点评:本题考查古典概型的计算,涉及茎叶图的作法与方差的计算,是基础题,解题时要牢记平均数、方差的公式,其次要正确运用列举法.

练习册系列答案
相关题目
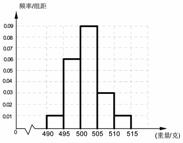 某食品厂为了检查甲乙两条自动包装流水线的生产情况,在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
某食品厂为了检查甲乙两条自动包装流水线的生产情况,在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.表1:(甲流水线样本频数分布表)
| 产品重量(克) | 频数 |
| (490,495] | 6 |
| (495,500] | 8 |
| (500,505] | 14 |
| (505,510] | 8 |
| (510,515] | 4 |
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
| 甲流水线 | 乙流水线 | 合计 | |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合计 | n= |
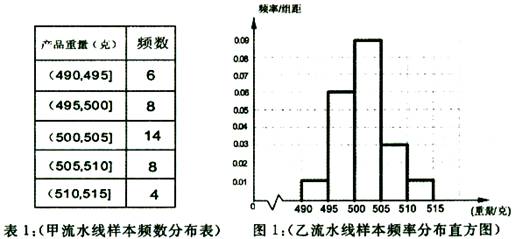
(本小题满分12分)品厂为了检查甲、乙两条自动包装流水线的生产情况,在这两条
流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]
的产品为合格品,否则为不合格品,表1是甲流水线样本频数分布表,图1是乙流水线样
本的频率分布直方图。
 某食
某食
(1)若检验员不小心将甲、乙两条流水线生产的重量值在(510,515]的产品放在了一起,
然后又随机取出3件产品,求至少有一件是乙流水线生产的产品的概率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为“产品的包装质量
与两条自动包装流水线的选择有关”。
|
|
甲流水线 |
乙流水线 |
合 计 |
|
合格品 |
a= |
b= |
|
|
不合格品 |
c= |
d= |
|
|
合 计 |
|
|
n= |