题目内容
已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中n=1,2,3,….(1)证明数列{lg(1+an)}是等比数列;
(2)设Tn=(1+a1)(1+a2)…(1+an),求Tn及数列{an}的通项;
(3)记bn=![]() +
+![]() ,求数列{bn}的前n项和Sn,并证明Sn+
,求数列{bn}的前n项和Sn,并证明Sn+![]() =1.
=1.
(1)证明:由已知an+1=an2+2an,∴an+1+1=(an+1)2.
∵a1=2,∴an+1>1,两边取对数得lg(1+an+1)=2lg(1+an),即![]() =2.∴{lg(1+an)}是公比为2的等比数列.
=2.∴{lg(1+an)}是公比为2的等比数列.
(2)解:由(1)知lg(1+an)=2n-1·lg(1+a1)=2n-1·lg3=lg32n-1.∴1+an=32n-1. (*)
∴Tn=(1+a1)(1+a2)…(1+an)=![]() ·…·
·…·![]() =
=![]() ,由(*)式得an=32n-1-1.
,由(*)式得an=32n-1-1.
(3)解:∵an+1=an2+2an,∴an+1=an(an+2).∴![]() .
.
∴![]()
![]()
![]() .
.
又bn=![]() +
+![]() ,
,
∴bn=2(![]()
![]() ).
).
∴Sn=b1+b2+…+bn=2(![]()
![]()
![]() )=2(
)=2(![]()
![]() ).
).
∵an=32n-1-1,a1=2,an+1=32n-1,∴Sn=1-![]() .又Tn=32n-1,∴Sn+
.又Tn=32n-1,∴Sn+![]() =1.
=1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
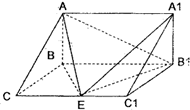 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,E为棱CC1的中点,已知AB=
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,E为棱CC1的中点,已知AB=