题目内容
某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题: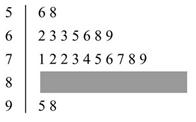
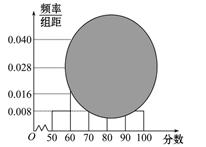
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高.
(1)25;(2)0.016.
解析试题分析:
解题思路:(1)通过茎叶图得出数据即可求解;(2)观察频率直方图中的各个矩形的高与面积即可.
规律总结:以图表给出的统计题目一般难度不大,主要考查频率直方图、茎叶图、频率分布表给出.
试题解析:(1)分数在[50,60)的频率为0.00810=0.08,由茎叶图知:分数在 [50,60)之间的频数为2,
所以全班人数为 =25.
=25.
(2)分数在[80,90)之间的频数为25-2-7-10-2=4,
频率分布直方图中 [80,90)间的矩形的高为 ÷10=0.016. .
÷10=0.016. .
考点:1.茎叶图;2.频率直方图.

某校学习小组开展“学生数学成绩与化学成绩的关系”的课题研究,对该校高二年级800名学生上学期期 数学和化学成绩,按优秀和不优秀分类得结果:数学和化学都优秀的有60人,数学成绩优秀但化学不优秀的有140人,化学成绩优秀但数学不优秀的有100人.
(Ⅰ)补充完整表格并判断能否在犯错概率不超过0.001前提下认为该校学生的数学成绩与化学成绩有关系?
| | 数学优秀 | 数学不优秀 | 总计 |
| 化学优秀 | | | |
| 化学不优秀 | | | |
| 总计 | | | |
(Ⅱ)4名成员随机分成两组,每组2人,一组负责收集成绩,另一组负责数据处理。求学生甲分到负责收集成绩组,学生乙分到负责数据处理组的概率。
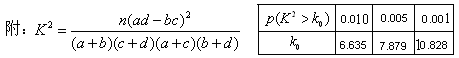
对某校小学生进行心理障碍测试得到如下的列联表:
| | 有心理障碍 | 没有心理障碍 | 总计 |
| 女生 | 10 | | 30 |
| 男生 | | 70 | 80 |
| 总计 | 20 | | 110 |
将表格填写完整,试说明心理障碍与性别是否有关?
附:

| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下
| | 男 | 女 | 合计 |
| 需要 | 40 | 30 | |
| 不需要 | 160 | 270 | |
| 合计 | | | |
(2)能否在犯错误的概率不超过0.01的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关系?
(3)根据(2)的结论,能否提出更好的调查方法估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由。
附表:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
随着工业化以及城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康,得到 列联表如下:
列联表如下:
| | 室外工作 | 室内工作 | 合计 |
| 有呼吸系统疾病 | 150 | | |
| 无呼吸系统疾病 | | 100 | |
| 合计 | 200 | | |
(1)补全
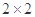 列联表;
列联表;(2)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1)根据以上数据建立一个 的列联表;(2)试判断成绩与班级是否有关?
的列联表;(2)试判断成绩与班级是否有关?
参考公式: ;
;
| P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
 列联表;
列联表;