Question

已知函数.

（1）试判断函数F（x）=(x²+1) f (x)—g(x)在[1，+∞)上的单调性；

（2）当0＜a＜b时，求证：函数f (x) 定义在区间[a,b]上的值域的长度大于（闭区间的长度定义为n –m）．

（3）方程f(x)=是否存在实数根？说明理由。

Answer 1

解（1）∵F（x）=(x²+1)lnx –2x+2．   ∴F ′（x）= 2xlnx+．

∴当x≥1时，F′（x）≥0且仅当x = 1时F′（x）= 0

∴F（x）在（1，+∞）上单调递增           

（2）∵0＜a＜b,f (x)在[a,b]上的值域为[lna,lnb]

∴要证值域的长度大于， 即证lnb – lna＞   只要证ln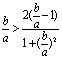

∵0＜a＜b,∴令  则只要证lnx＞  （x>1）

即证（x²+1）lnx –(2x –2)>0  (※)

由（1）可知F(x)在（1，+∞）上单调递增 ∴F（x）＞F（1）= 0 所以（※）式成立．

∴f (x)在[a, b]上的值域的长度大于．

（3）∵f (x) =         xlnx=

令h (x) = xlnx(x>0)．则h ′（x）=lnx+1    当x∈（0，）时h ′（x）< 0,     h (x)单调递减；

当x∈（）时，h′（x）>0，h (x)单调递增．所以h (x)_min= h ()= –．

令(x)=则

当x∈（0，1），，单调递增；   当x∈（1，+∞）时，，单调递减．

∴_max=            所以方程f(x)= 没有实根