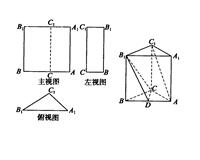
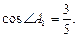题目内容
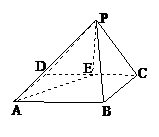
如图,底面是正方形的四棱锥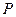 –
–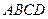 ,平面
,平面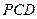 ⊥平面
⊥平面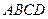 ,
,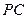 =
=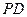 =
=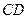 =2.
=2.
(I)求证: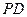 ⊥
⊥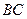 ;
;
(II)求直线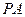 与平面
与平面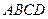 所成的角的正弦值.
所成的角的正弦值.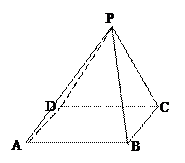
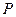 –
–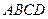 ,平面
,平面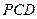 ⊥平面
⊥平面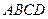 ,
,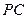 =
=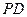 =
=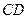 =2.
=2.(I)求证:
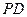 ⊥
⊥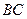 ;
;(II)求直线
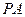 与平面
与平面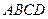 所成的角的正弦值.
所成的角的正弦值.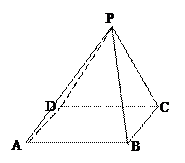
(II)
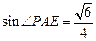
(I)证明:∵平面
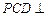 平面
平面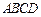 ,
,平面
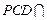 平面
平面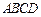 =
=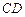 ,
,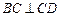 ,∴
,∴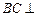 平面
平面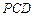 ,
, 又
又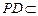 平面
平面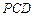 ,∴
,∴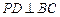 ..………………………………7 分
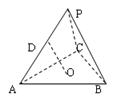
..………………………………7 分(II)取
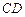 中点
中点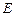 ,由
,由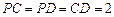 得
得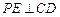 ,
,又平面
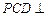 平面
平面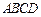 ,故
,故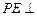 平面
平面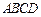 ,
,∴
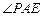 就是直线
就是直线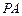 与平面
与平面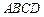 所成的角.
所成的角.∵
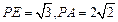 ,∴
,∴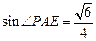 . ……………………………………14 分
. ……………………………………14 分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
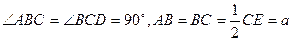 ,D是CE的中点,点M和点N在
,D是CE的中点,点M和点N在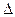 ADE绕AD向上翻折的过程中,分别以
ADE绕AD向上翻折的过程中,分别以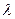 的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0
的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0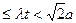 。
。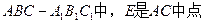 .
.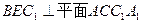 ;
;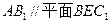 ;
;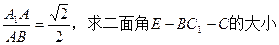 .
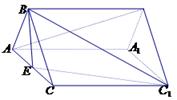
.
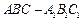 中,
中,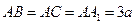 ,
, 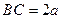 ,
,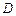 是
是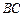 的中点,
的中点,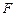 是
是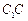 上一点,且
上一点,且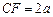 .
.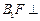 平面
平面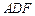 ;
;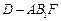 的体积;
的体积;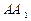 上找一点
上找一点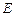 ,使得
,使得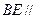 平面
平面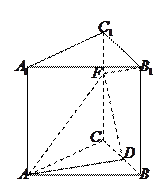
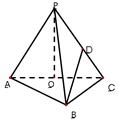
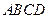 中,底面
中,底面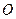 是正方形
是正方形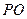
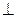 底面
底面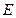 是
是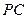 的中点.
的中点.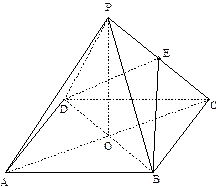
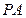 ∥平面
∥平面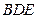 ;
;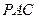
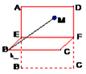
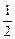 ,那么点M到直线EF的距离为( )
,那么点M到直线EF的距离为( )