题目内容
4.P到$(0,\sqrt{3}),(0,-\sqrt{3})$距离之和为4,设点P的轨迹为C,直线y=kx+1与C交于AB(Ⅰ)求C的方程
(Ⅱ)若$\overrightarrow{OA}⊥\overrightarrow{OB}$,求k.
分析 (Ⅰ)设P(x,y),由椭圆定义可知其轨迹为椭圆;
(Ⅱ)设A(x1,y1),B(x2,y2),联立化为(k2+4)x2+2kx-3=0.由$\overrightarrow{OA}⊥\overrightarrow{OB}$,可得x1x2+y1y2=0.把根与系数的关系代入即可得出.
解答 解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以$(0,-\sqrt{3}),(0,\sqrt{3})$为焦点,长半轴为2的椭圆.
它的短半轴$b=\sqrt{{2^2}-{{(\sqrt{3})}^2}}=1$,
故曲线C的方程为${x^2}+\frac{y^2}{4}=1$.
(Ⅱ)设A(x1,y1),B(x2,y2),其坐标满足$\left\{\begin{array}{l}{x^2}+\frac{y^2}{4}=1\\ y=kx+1.\end{array}\right.$
消去y并整理得(k2+4)x2+2kx-3=0,
故${x_1}+{x_2}=-\frac{2k}{{{k^2}+4}},{x_1}{x_2}=-\frac{3}{{{k^2}+4}}$
若$\overrightarrow{OA}⊥\overrightarrow{OB}$,即x1x2+y1y2=0.
而${y_1}{y_2}={k^2}{x_1}{x_2}+k({x_1}+{x_2})+1$,
于是${x_1}{x_2}+{y_1}{y_2}=-\frac{3}{{{k^2}+4}}-\frac{{3{k^2}}}{{{k^2}+4}}-\frac{{2{k^2}}}{{{k^2}+4}}+1=0$,化简得-4k2+1=0,
解得$k=±\frac{1}{2}$.
点评 本题考查了向量垂直与数量积的关系、椭圆的定义及其标准方程、直线与椭圆相交问题、一元二次的根与系数的关系,考查了推理能力与计算能力,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案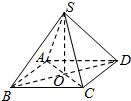 如图,已知四棱锥S-ABCD的侧棱与底面边长都是2,且底面ABCD是正方形,则侧棱与底面所成的角( )
如图,已知四棱锥S-ABCD的侧棱与底面边长都是2,且底面ABCD是正方形,则侧棱与底面所成的角( )| A. | 75° | B. | 60° | C. | 45° | D. | 30° |