Question

设非零向量

OA

，

OB

满足|

OA

+

OB

|=|

OA

-

OB

|=4，则△AOB面积的最大值为（　　）

• A、36
• B、24
• C、12
• D、4

Answer 1

分析：设|

OA

|=x，|

OB

|=y，由题意结合向量的加减法则可得x²+y²=16，由基本不等式可得其最值．

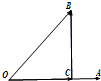
解答：解：如图，由向量加减法则可得

OC

=

OA

+

OB

，

BA

=

OA

-

OB

，
∵|

OA

+

OB

|=|

OA

-

OB

|=4，
∴四边形OBCA为矩形，
设|

OA

|=x，|

OB

|=y，则可得x²+y²=16，
而△AOB面积S=

1

2

xy≤

1

2

•

x2+y2

2

=4，
当且仅当x=y=2

2

时，上式取等号，
故△AOB面积的最大值为4
故选：D

点评：本题考查平面向量的运算，涉及三角形的面积公式和基本不等式求最值，属中档题．