题目内容
设常数 ,则a= ;
,则a= ; (a+a2+…an)= .
(a+a2+…an)= .
【答案】分析:(1)利用二项展开式通项公式Tr+1=c4r(ax2)4-r( )r,整理后,令x的次数等于3,从而解得a,
)r,整理后,令x的次数等于3,从而解得a,
(2)由a= <1,可知数列a,a2…an是递降等比数列,则
<1,可知数列a,a2…an是递降等比数列,则  (a+a2+…+an)表示无穷递降等比数列的各项和,利用无穷递降等比数列的各项和公式,可得解.
(a+a2+…+an)表示无穷递降等比数列的各项和,利用无穷递降等比数列的各项和公式,可得解.
解答:解:(1)由Tr+1=c4r(ax2)4-r( )r,整理得Tr+1=c4ra4-rx8-
)r,整理得Tr+1=c4ra4-rx8- r,
r,
r=2时,即c42a2= ,∴a=
,∴a= .
.
故答案为: .
.
(2)由a= ,可知数列a,a2…an是递降等比数列,
,可知数列a,a2…an是递降等比数列,
则 (a+a2+…+an)表示无穷递降等比数列的各项和,
(a+a2+…+an)表示无穷递降等比数列的各项和,
由无穷递降等比数列的各项和公式( sn=
sn= ),
),
可知 (a+a2+…+an)=
(a+a2+…+an)= ═
═ =1.
=1.
故答案为:1.
点评:本题(1)主要考查二项式展开式特定项的系数的求法,需要熟记展开式的通项公式,即Tr+1=cnran-rbr.是高考的常见题型.
(2)主要考查等比数列求和公式及极限的运算,需要注意:当a的绝对值小于1时, an=0,要记住无穷递降等比数列各项和公式
an=0,要记住无穷递降等比数列各项和公式  sn=
sn= .在选择填空中可以加快速度.
.在选择填空中可以加快速度.
 )r,整理后,令x的次数等于3,从而解得a,
)r,整理后,令x的次数等于3,从而解得a,(2)由a=
 <1,可知数列a,a2…an是递降等比数列,则
<1,可知数列a,a2…an是递降等比数列,则  (a+a2+…+an)表示无穷递降等比数列的各项和,利用无穷递降等比数列的各项和公式,可得解.
(a+a2+…+an)表示无穷递降等比数列的各项和,利用无穷递降等比数列的各项和公式,可得解.解答:解:(1)由Tr+1=c4r(ax2)4-r(
 )r,整理得Tr+1=c4ra4-rx8-
)r,整理得Tr+1=c4ra4-rx8- r,
r,r=2时,即c42a2=
 ,∴a=
,∴a= .
.故答案为:
 .
.(2)由a=
 ,可知数列a,a2…an是递降等比数列,
,可知数列a,a2…an是递降等比数列,则
 (a+a2+…+an)表示无穷递降等比数列的各项和,
(a+a2+…+an)表示无穷递降等比数列的各项和,由无穷递降等比数列的各项和公式(
 sn=
sn= ),
),可知
 (a+a2+…+an)=
(a+a2+…+an)= ═
═ =1.
=1.故答案为:1.
点评:本题(1)主要考查二项式展开式特定项的系数的求法,需要熟记展开式的通项公式,即Tr+1=cnran-rbr.是高考的常见题型.
(2)主要考查等比数列求和公式及极限的运算,需要注意:当a的绝对值小于1时,
 an=0,要记住无穷递降等比数列各项和公式
an=0,要记住无穷递降等比数列各项和公式  sn=
sn= .在选择填空中可以加快速度.
.在选择填空中可以加快速度. 
练习册系列答案
相关题目
 为定义在
为定义在 上的奇函数,当
上的奇函数,当 时,
时, (
( 为常数),则
为常数),则

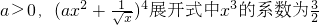 ,则a=________;
,则a=________;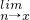 (a+a2+…an)=________.
(a+a2+…an)=________. ,则a=( );
,则a=( ); (a+a2+…an)=( )
(a+a2+…an)=( )