题目内容
【题目】设数列满足|an﹣ 
|≤1，n∈N* ．
（1）求证：|an|≥2n﹣1（|a1|﹣2）（n∈N*）
（2）若|an|≤（ 
）n ， n∈N* ， 证明：|an|≤2，n∈N* ．
【答案】
（1）
解：∵|an﹣ 
|≤1，∴|an|﹣ 
|an+1|≤1，
∴ 
﹣ 
≤ 
，n∈N*，
∴ 
=（ 
）+（ 
）+…+（ 
）≤ + 
+ 
+…+ = 
=1﹣ ＜1．
∴|an|≥2n﹣1（|a1|﹣2）（n∈N*）
（2）
解：任取n∈N*，由（1）知，对于任意m＞n，
﹣ 
=（ 
）+（ 
）+…+（ 
）
≤ + 
+…+ 
= 
＜ 
．
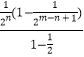∴|an|＜（ + ）2n≤[ + 
（ 
）m]2n=2+（ 
）m2n．①
由m的任意性可知|an|≤2．
否则，存在n0∈N*，使得| 
|＞2，
取正整数m0＞ 
且m0＞n0，则
＜ （ ） =| |﹣2，与①式矛盾．
综上，对于任意n∈N*，都有|an|≤2
【解析】（1）使用三角不等式得出|an|﹣ 
|an+1|≤1，变形得 
﹣ 
≤ 
，使用累加法可求得 
＜1，即结论成立；（2）利用（1）的结论得出 
﹣ 
＜ 
，进而得出|an|＜2+（ 
）m2n ， 利用m的任意性可证|an|≤2．本题考查了不等式的应用与证明，等比数列的求和公式，放缩法证明不等式，难度较大．
名校课堂系列答案【题目】已知函数f（x）=（ex+1）（ax+2a﹣2），若存在x∈（0，+∞），使得不等式f（x）﹣2＜0成立，则实数a的取值范围是（ ）
A.（0，1）
B.（0， 
）
C.（﹣∞，1）
D.（﹣∞， ）
【题目】为了解男性家长和女性家长对高中学生成人礼仪式的接受程度，某中学团委以问卷形式调查了
位家长，得到如下统计表：
男性家长 | 女性家长 | 合计 | |
赞成 |
|
|
|
无所谓 |
|
|
|
合计 |
|
|
|
（1）据此样本，能否有
的把握认为“接受程度”与家长性别有关？说明理由；
（2）学校决定从男性家长中按分层抽样方法选出
人参加今年的高中学生成人礼仪式，并从中选
人交流发言，求发言人中至多一人持“赞成”态度的概率.
