题目内容
已知函数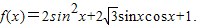 求:
求:(Ⅰ)f(x)的最小正周期;
(Ⅱ)f(x)的单调递增区间;
(Ⅲ)f(x)在
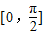 上的最值.
上的最值.
【答案】分析:(1)先将函数化简为:f(x)=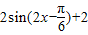 ,根据最小正周期的求法即可得到答案.
,根据最小正周期的求法即可得到答案.
(2)根据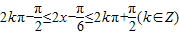 ,可求出答案.
,可求出答案.
(3)根据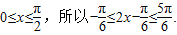 再由三角函数的单调性可的答案.
再由三角函数的单调性可的答案.
解答:解:(Ⅰ)因为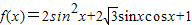 =
=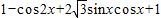
=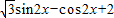
=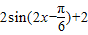 ,
,
所以f(x)的最小正周期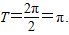
(Ⅱ)因为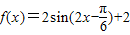 ,
,
所以由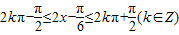 ,
,
得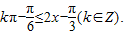
所以f(x)的单调增区间是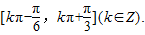
(Ⅲ)因为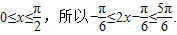
所以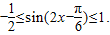
所以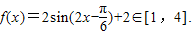
即f(x)的最小值为1,最大值为4.
点评:本题主要考查三角函数最小正周期的求法、单调区间的求法以及在限定区间上的三角函数的最值的求法.这种题型首先将函数化简为:y=Asin(ωx+φ)的形式后进行解题.
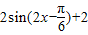 ,根据最小正周期的求法即可得到答案.
,根据最小正周期的求法即可得到答案.(2)根据
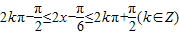 ,可求出答案.
,可求出答案.(3)根据
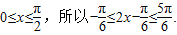 再由三角函数的单调性可的答案.
再由三角函数的单调性可的答案.解答:解:(Ⅰ)因为
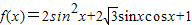 =
=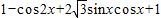
=
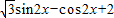
=
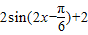 ,
,所以f(x)的最小正周期
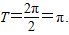
(Ⅱ)因为
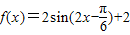 ,
,所以由
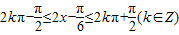 ,
,得
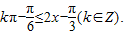
所以f(x)的单调增区间是
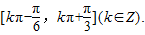
(Ⅲ)因为
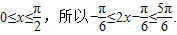
所以
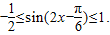
所以
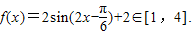
即f(x)的最小值为1,最大值为4.
点评:本题主要考查三角函数最小正周期的求法、单调区间的求法以及在限定区间上的三角函数的最值的求法.这种题型首先将函数化简为:y=Asin(ωx+φ)的形式后进行解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 求:
求: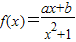 在点(-1,f(-1))的切线方程为x+y+3=0.
在点(-1,f(-1))的切线方程为x+y+3=0.