题目内容

已知三个平面α、β、γ两两互相平行,点A、D∈α,点C、F∈γ,线段AC、DF分别交平面β于B、E两点,试证明

思路解析：如图,作辅助线AF交平面β于点G,连结BG、GE.这样就把AB、DF联系起来了,在△ACF和△FAD中利用比例关系得到结论.

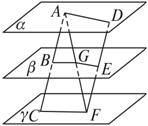
证明：如图,连结AF交平面β于点G,连结BG、GE.

∵α∥β∥γ,∴BG∥CF.∴                          ①

同理,由α∥β∥γ,得GE∥AD.∴                  ②

由①②,得.

误区警示  做本题时,容易误认为A、C、D、F四点可构成一个平面,而这一条件是题设中所没有的,这就犯了无中生有的错误.


练习册系列答案
相关题目
5、已知三个平面α、β、γ，若β⊥γ，且α与β、α与γ均相交但不垂直，a、b分别为α、β内的直线，则（　　）
5、已知三个平面α，β，γ，若β⊥γ，且α与γ相交但不垂直，a，b分别为α，β内的直线，则（　　）
已知三个平面向量
AB
、
AC
、
BC
满足|
AB
|=1，|
AC
|=2，|
BC
|=
3
，点E是BC的中点，若点D满足
BD
=2
AE
，则
AC
•
CD
=
2
2
．
已知三个平面α，β，γ两两相交于三条直线，即α∩β=c，β∩γ=a，γ∩α=b，若a和b不平行．求证：a，b，c必过同一点．
已知三个平面两两互相垂直且交于一点O，若空间一点P到这三个平面的距离分别为2，3，6，则OP 的长是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网