题目内容
求值:(1)sin6°sin42°sin66°sin78°;
(2)sin220°+cos250°+sin20°cos50°.
分析:(1)先利用诱导公式化简可得sin6°cos12°cos24°cos48°,考虑到题目中的角成二倍角,故添项cos6°,配凑二倍角的正弦,从而可求
(2)利用二倍角的余弦公式及积化和差公式、和差化积公式,化简可得
(2)利用二倍角的余弦公式及积化和差公式、和差化积公式,化简可得
解答:解:(1)原式=sin6°cos12°cos24°cos48°
=
=
=
=
=
=
(2)原式=
+
+
(sin70°-sin30°)
=1+
(cos1000-cos400)+
sin700-
=
-sin70°sin30°+
sin70°=
=
| sin6°cos6°cos12°cos24°cos48° |
| cos6° |
=
| ||
| cos6° |
=
| ||
| cos6° |
=
| ||
| cos6° |
| ||
| cos6° |
| 1 |
| 16 |
(2)原式=
| 1-cos40° |
| 2 |
| 1+cos100° |
| 2 |
| 1 |
| 2 |
=1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
=
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
点评:本题主要考查了三角函数的化简与求值,综合运用了二倍角的正弦公式,二倍角的余弦公式,和差化积、积化和差、等公式的综合运用.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
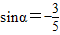 ,且α为第三象限角,求cosα,cos2α的值
,且α为第三象限角,求cosα,cos2α的值