Question

函数f(x)=

x2-2x+1，(x＞0) -x2-ax-1，(x＜0)

是奇函数，则实数a=

 

．

Answer 1

分析：题目给出的函数是分段函数，函数又是奇函数，其图象关于原点中心对称，对应的两段函数的顶点关于原点对称，则原点横坐标互为相反数，由此可以求得a的值．

解答：解：因为函数f(x)=

x2-2x+1(x＞0) -x2-ax-1(x＜0)

是奇函数，
所以函数的图象关于原点中心对称，如图，

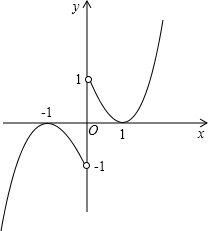
当x＞0时，函数f（x）=x²-2x+1的图象是开口向上的抛物线的部分，
当x＜0时，函数f（x）=-x²-ax-1的图象是开口向下的抛物线的部分，
要使图象关于原点对称，则其顶点关于原点对称，
所以有顶点的横坐标互为相反数，即-

-2

2×1

=-(-

-a

2×(-1)

)，所以a=2．
故答案为2．

点评：本题考查了分段函数的奇偶性，分段函数奇偶性的判断需要分段进行，也可借助于图象进行分析，利用图象分析使问题更加直观．此题是基础题．