题目内容
已知 ,则
,则 的取值范围为________.
的取值范围为________.

分析:把
 看成是定点A(-6,0)与椭圆
看成是定点A(-6,0)与椭圆 上动点P连线的斜率,且过定点A(-6,0)的直线与椭圆一定有交点,先求出直线与椭圆有交点的特殊情况,即直线与椭圆相切时的t值,其它情况应在两条切线之间,即可求出范围.
上动点P连线的斜率,且过定点A(-6,0)的直线与椭圆一定有交点,先求出直线与椭圆有交点的特殊情况,即直线与椭圆相切时的t值,其它情况应在两条切线之间,即可求出范围.解答:
 可以斜率,
可以斜率, 的取值范围为过定点
的取值范围为过定点A(-6,0)与椭圆相切的两直线斜率之间.
设过定点A(-6,0)的直线方程为y=k(x+6),代入椭圆方程,得,(
 +
+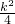 )x2+3k2x+9k2-1=0
)x2+3k2x+9k2-1=0∵y=k(x+6)与椭圆相切,∴△=0.即9k4-4(
 )(9k2-1)=0
)(9k2-1)=0解得,k=±
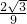 .
.当过定点A(-6,0)的直线与椭圆有交点时,可看出斜率在-
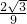 到
到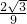 之间.
之间.故答案为

点评:本题考查了利用
 的几何意义,以及直线与椭圆切线求法,求t范围做题时应认真分析,找到切入点.
的几何意义,以及直线与椭圆切线求法,求t范围做题时应认真分析,找到切入点. 
练习册系列答案
相关题目
 ,则的取值范围为
,则的取值范围为
 <x<2
D . 0<x<2
<x<2
D . 0<x<2 ,则
,则 的取值范围为_____
的取值范围为_____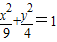 ,则
,则 的取值范围为 .
的取值范围为 . ,则
,则 的取值范围为 .
的取值范围为 .