题目内容
【题目】在平面直角坐标系![]() 中,由
中,由![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,以原点为极点,
,以原点为极点,![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程以及曲线
的极坐标方程以及曲线![]() 的直角坐标方程;
的直角坐标方程;
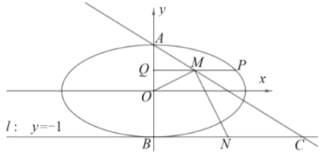
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 与曲线
与曲线![]() 、曲线
、曲线![]() 在第一象限交于
在第一象限交于![]() 、
、![]() ,且
,且![]() ,点
,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]()
![]() ;
;![]() (x﹣2)2+y2=4;(2)
(x﹣2)2+y2=4;(2)![]() .
.
【解析】
(1)直接利用伸缩变换的应用和参数方程极坐标方程和直角坐标方程之间的转换求出结果.
(2)利用三角俺和你熟关系式的变换和极径的应用及三角形的面积公式的应用求出结果.
解:(1)平面直角坐标系![]() 中,由
中,由![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,得到直角坐标方程为
,得到直角坐标方程为![]() .
.
根据 转换为极坐标方程为
转换为极坐标方程为![]() .
.
曲线![]() 的极坐标方程为
的极坐标方程为![]() .根据
.根据 转换为直角坐标方程为
转换为直角坐标方程为![]() .
.
(2)由于 得到:
得到:![]() ,
,
且![]() 整理得
整理得![]() .
.
由于![]() ,
,
所以![]() ,
,
故:![]() ,解得
,解得![]() .
.
所以![]() ,
,![]() .
.
则:![]()
![]() .
.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目