题目内容
数列{an}的通项公式是an=n2-7n+6.
(1)这个数列的第4项是多少?
(2)150是不是这个数列的项?若是这个数列的项,它是第几项?
(3)该数列从第几项开始各项都是正数?
解析:(1)当n=4时,a4=42-4×7+6=-6.
(2)令an=150,即n2-7n+6=150,解得n=16,即150是这个数列的第16项.
(3)令an=n2-7n+6>0,解得n>6或n<1(舍),
∴从第7项起各项都是正数.
14.已知各项均为正数的数列{an}的前n项和满足Sn>1,且6Sn=(an+1)(an+2),n∈N*.求{an}的通项公式.
解析 由a1=S1=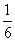 (a1+1)(a1+2),
(a1+1)(a1+2),
解得a1=1或a1=2,由已知a1=S1>1,因此a1=2.
又由an+1=Sn+1-Sn
=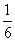 (an+1+1)(an+1+2)-
(an+1+1)(an+1+2)-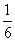 (an+1)(an+2),
(an+1)(an+2),
得an+1-an-3=0或an+1=-an.
因an>0,故an+1=-an不成立,舍去.
因此an+1-an-3=0.
即an+1-an=3,从而{an}是公差为3,首项为2的等差数列,故{an}的通项为an=3n-1.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目

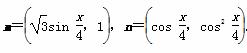
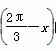 的值;
的值; ,
, ,-
,- ,…的一个通项公式是( )
,…的一个通项公式是( )
 中,令x=1,2,3,…,得到一个数列,则这个数列的前5项是________.
中,令x=1,2,3,…,得到一个数列,则这个数列的前5项是________.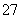 +2a11=0,数列{bn}是等比数列,且b7=a7,则b6b8=________.
+2a11=0,数列{bn}是等比数列,且b7=a7,则b6b8=________. 中,点
中,点 在棱
在棱 的延长线上,
的延长线上, 且
且 .
. //平面
//平面 ;
;
 平面
平面 ;
; 的体积.
的体积.