题目内容
设抛物线 ,
,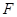 为焦点,
为焦点,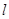 为准线,准线与
为准线,准线与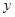 轴交点为
轴交点为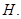
(1)求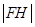 ;
;
(2)过点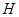 的直线与抛物线
的直线与抛物线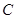 交于
交于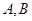 两点,直线
两点,直线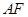 与抛物线交于点
与抛物线交于点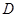 .
.
①设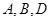 三点的横坐标分别为
三点的横坐标分别为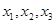 ,计算:
,计算: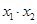 及
及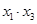 的值;
的值;
②若直线 与抛物线交于点
与抛物线交于点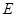 ,求证:
,求证: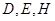 三点共线.
三点共线.
【答案】
(1)  (2)
(2)  ,
, ,并根据斜率相等来证明三点共线。
,并根据斜率相等来证明三点共线。
【解析】
试题分析:(1)
(2)设直线 方程:
方程: ,直线
,直线 方程:
方程:






设


 三点共线。
三点共线。
考点:直线与抛物线的位置关系
点评:解决的关键是利用抛物线的定义,以及联立方程组的思想来得到根与系数的关系,结合点的坐标来求解斜率,确定点的位置,属于基础题。

练习册系列答案
相关题目
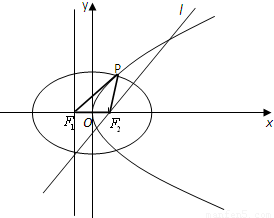
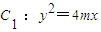 (m>0)的准线与x轴交于F1,焦点为F2;以F1、F2为焦点,离心率
(m>0)的准线与x轴交于F1,焦点为F2;以F1、F2为焦点,离心率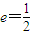 的椭圆C2与抛物线C1的一个交点为P.
的椭圆C2与抛物线C1的一个交点为P.