题目内容
某抛物线形拱桥跨度是20米,拱高4米,在建桥时每隔4米需用一支柱支撑,求其中最长的支柱的长. 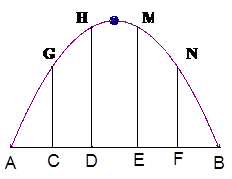

3. 84米。
试题分析:以拱顶为原点,水平线为
 轴,建立坐标系,
轴,建立坐标系,
如图,由题意知,
 ,
, 、
、 坐标分别为
坐标分别为 、
、
设抛物线方程为
 ,将
,将 点坐标代入,得
点坐标代入,得
解得
 ,于是抛物线方程为
,于是抛物线方程为 .
. 由题意知
 点坐标为
点坐标为 ,
, 点横坐标也为2,将2代入得
点横坐标也为2,将2代入得
从而
 故最长支柱长应为3. 84米。
故最长支柱长应为3. 84米。点评:对于实际应用题,首先应审清题意,找出各量之间的关系,建立数学模型性,然后用数学的方法解答,并回到实际问题中验证其正确性。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
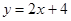 与抛物线
与抛物线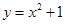 所围成封闭图形的面积是( )
所围成封闭图形的面积是( )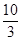
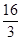
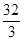
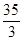
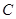 的顶点为原点,其焦点
的顶点为原点,其焦点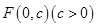 到直线
到直线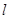 :
: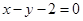 的距离为
的距离为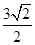 .设
.设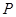 为直线
为直线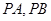 ,其中
,其中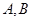 为切点.
为切点.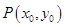 为直线
为直线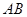 的方程;
的方程;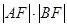 的最小值.
的最小值.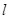 过点
过点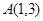 , 且直线
, 且直线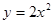 交于
交于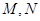 两点. 若
两点. 若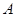 点恰好是
点恰好是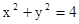 上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线
上各点的纵坐标变为原来的一半 (横坐标不变), 得到曲线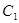 、抛物线
、抛物线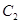 的焦点是直线y=x-1与x轴的交点.
的焦点是直线y=x-1与x轴的交点. 满足条件:① 过
满足条件:① 过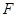 ;②与
;②与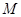 ,
,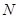 ,且满足
,且满足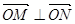 ?若存在,求出直线
?若存在,求出直线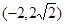 ,则抛物线的方程是
,则抛物线的方程是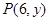 在抛物线
在抛物线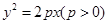 上,
上,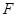 为抛物线焦点, 若
为抛物线焦点, 若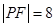 , 则点
, 则点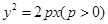 的焦点,与抛物线交于两点A、B, 将直线
的焦点,与抛物线交于两点A、B, 将直线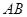 按向量
按向量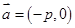 平移得到直线
平移得到直线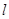 ,
,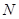 为
为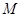 为抛物线弧
为抛物线弧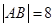 ,求抛物线方程.
,求抛物线方程. 的最大值.
的最大值. 的最小值.
的最小值.