题目内容

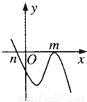
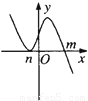
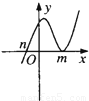
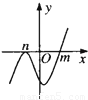
设m＞n，函数y=（x-m）2（n-x）的图象可能是


  1. A.
  2. B.
  3. C.
  4. D.
A
分析：根据函数在（m，+∞）上是减函数，排除C、D，再根据x=m使y′=0，函数取得极值，故排除B，从而得到正确的选项
解答：由于m＞n，函数y=（x-m）2（n-x）当x＞m时，函数值随着x的增大而减小，故函数在（m，+∞）上是减函数，
故排除C、D．
由于y′=（x-m）（2n+m-3x），故x=m使y′=0，函数取得极值，故排除B，只有A满足条件，
故选A．
点评：本题主要考查利用函数的单调性和极值判断函数的图象，属于基础题．
练习册系列答案
相关题目
设m＞n，函数y=（x-m）2（n-x）的图象可能是（　　）
（2011•顺义区二模）对于定义域分别为M，N的函数y=f（x），y=g（x），规定：
函数h(x)=
f(x)•g(x)，当x∈M且x∈N
f(x)，当x∈M且x∉N
g(x)，当x∉M且x∈N

（1）若函数f(x)=
1
x+1
，g(x)=x2+2x+2，x∈R，求函数h（x）的取值集合；
（2）若f（x）=1，g（x）=x2+2x+2，设bn为曲线y=h（x）在点（an，h（an））处切线的斜率；而{an}是等差数列，公差为1（n∈N*），点P1为直线l：2x-y+2=0与x轴的交点，点Pn的坐标为（an，bn）．求证：
1
|P1P2|2
+
1
|P1P3|2
+…+
1
|P1Pn|2
＜
2
5
；
（3）若g（x）=f（x+α），其中α是常数，且α∈[0，2π]，请问，是否存在一个定义域为R的函数y=f（x）及一个α的值，使得h（x）=cosx，若存在请写出一个f（x）的解析式及一个α的值，若不存在请说明理由．
对于定义域为I的函数y=f（x），如果存在区间[m，n]⊆I，同时满足：①f（x）在[m，n]内是单调函数；②当定义域是[m，n]，f（x）值域也是[m，n]，则称[m，n]是函数y=f（x）的“好区间”．
（1）设g(x)=loga(ax-2a)+loga(ax-3a)（其中a＞0且a≠1），判断g（x）是否存在“好区间”，并说明理由；
（2）已知函数P(x)=
(t2+t)x-1t2x
(t∈R，t≠0)有“好区间”[m，n]，当t变化时，求n-m的最大值．
设m＞n，函数y=（x-m）2（n-x）的图象可能是（ ）
A．
B．
C．
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网