题目内容
对于定义域为I的函数y=f(x),如果存在区间[m,n]⊆I,同时满足:①f(x)在[m,n]内是单调函数;②当定义域是[m,n],f(x)值域也是[m,n],则称[m,n]是函数y=f(x)的“好区间”.
(1)设g(x)=loga(ax-2a)+loga(ax-3a)(其中a>0且a≠1),判断g(x)是否存在“好区间”,并说明理由;
(2)已知函数P(x)=
(t∈R,t≠0)有“好区间”[m,n],当t变化时,求n-m的最大值.
(1)设g(x)=loga(ax-2a)+loga(ax-3a)(其中a>0且a≠1),判断g(x)是否存在“好区间”,并说明理由;
(2)已知函数P(x)=
| (t2+t)x-1 | t2x |
分析:(1)g(x)在区间[m,n]是单调的,由g(m)=m,g(n)=n得m、n是方程g(x)=x的两个不等实根,从而求出a的取值范围;
(2)函数P(x)有“好区间”[m,n],即P(x)在[m,n]上是单调函数,由
得m,n是方程P(x)=x的同号不等二实根,求得n-m的最大值.
(2)函数P(x)有“好区间”[m,n],即P(x)在[m,n]上是单调函数,由
|
解答:解:(1)由题意,
,∴ax>3a,(a>0且a≠1);
①当a>1时,x>loga(3a),此时D=(loga(3a),+∞),任取x1、x2∈D,且x1<x2,
∵ax1<ax2,∴0<ax1-2a<ax2-2a,0<ax1-3a<ax2-3a,
∴loga(ax1-2a)<loga(ax2-2a),loga(ax1-3a)<loga(ax2-3a);
∴g(x)在D=(loga(3a),+∞)上是增函数;
②当0<a<1时,x<loga(3a),此时D=(-∞,loga(3a)),
同理可证,g(x)在D=(-∞,loga(3a))上是增函数;
∴存在好区间[m,n]?存在m,n∈D(m<n),使
成立,
等价于关于x的方程f(x)=x在定义域D上有两个不等实根,
即(ax-2a)(ax-3a)=ax(*)在定义域D上有两个不等实根;
设t=ax,t∈D,则(*)等价于方程(t-2a)(t-3a)=t,
即t2-(5a+1)t+6a2=0在(3a,+∞)上有两个不等实根,
设函数h(t)=t2-(5a+1)t+6a2,则
无解;
∴函数g(x)不存在好区间;
(2)∵函数P(x)=
(t∈R,t≠0)有“好区间”[m,n],
∴[m,n]?(-∞,0)或[m,n]?(0,+∞);
∴P(x)=
-
在[m,n]上单调递增,
∴
,即m,n是方程P(x)=x的同号不等二实根,
即方程t2x2-t(t+1)x+1=0,
∵mn=
>0,
∴△=t2(t+1)2-4t2>0,
∴t>1或t<-3,
∴n-m=
=
,其中t∈(-∞,-3)∪(1,+∞);
当t=3时,n-m取得最大值
.
|
①当a>1时,x>loga(3a),此时D=(loga(3a),+∞),任取x1、x2∈D,且x1<x2,
∵ax1<ax2,∴0<ax1-2a<ax2-2a,0<ax1-3a<ax2-3a,
∴loga(ax1-2a)<loga(ax2-2a),loga(ax1-3a)<loga(ax2-3a);
∴g(x)在D=(loga(3a),+∞)上是增函数;
②当0<a<1时,x<loga(3a),此时D=(-∞,loga(3a)),
同理可证,g(x)在D=(-∞,loga(3a))上是增函数;
∴存在好区间[m,n]?存在m,n∈D(m<n),使
|
等价于关于x的方程f(x)=x在定义域D上有两个不等实根,
即(ax-2a)(ax-3a)=ax(*)在定义域D上有两个不等实根;
设t=ax,t∈D,则(*)等价于方程(t-2a)(t-3a)=t,
即t2-(5a+1)t+6a2=0在(3a,+∞)上有两个不等实根,
设函数h(t)=t2-(5a+1)t+6a2,则
|
∴函数g(x)不存在好区间;
(2)∵函数P(x)=
| (t2+t)x-1 |
| t2x |
∴[m,n]?(-∞,0)或[m,n]?(0,+∞);
∴P(x)=
| t+1 |
| t |
| 1 |
| t2x |
∴
|
即方程t2x2-t(t+1)x+1=0,
∵mn=
| 1 |
| t2 |
∴△=t2(t+1)2-4t2>0,
∴t>1或t<-3,
∴n-m=
| (m+n)2-4mn |
-3(
|
当t=3时,n-m取得最大值
2
| ||
| 3 |
点评:本题考查了利用导数研究函数的单调性以及根据函数的单调性判定一元二次方程根的情况,是易错题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
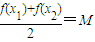 ,则称M为函数y=f (x)的“均值”.
,则称M为函数y=f (x)的“均值”.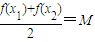 ,则称M为函数y=f (x)的“均值”.
,则称M为函数y=f (x)的“均值”.