题目内容
 如图,半径为1的圆与直线l相交于A、B两个不同的点,设∠AOB=x,当直线l平行移动时,则圆被直线扫过部分(图中阴影部分)的面积s关于x的函数s(x)=
如图,半径为1的圆与直线l相交于A、B两个不同的点,设∠AOB=x,当直线l平行移动时,则圆被直线扫过部分(图中阴影部分)的面积s关于x的函数s(x)=| 1 |
| 2 |
| 1 |
| 2 |
分析:根据图形可知,图中阴影部分的面积s等于扇形的面积减去三角形的面积,利用公式分别计算扇形的面积、三角形的面积即可
解答:解:由题意,图中阴影部分的面积s等于扇形的面积减去三角形的面积
∵扇形的面积为
x,三角形的面积为
sinx
∴s=
(x-sinx),x∈(0,2π)
故答案为
(x-sinx),x∈(0,2π)
∵扇形的面积为
| 1 |
| 2 |
| 1 |
| 2 |
∴s=
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题的考点是函数模型的选择与应用,主要考查函数模型的建立,考查扇形的面积,三角形的面积公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
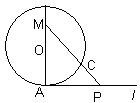 如图,已知圆心为O,半径为1的圆与直线l相切于点A,一动点P自切点A沿直线l向右移动时,取弧AC的长为
如图,已知圆心为O,半径为1的圆与直线l相切于点A,一动点P自切点A沿直线l向右移动时,取弧AC的长为 二面角
二面角 内半径为1的圆
内半径为1的圆 与半径为2的圆
与半径为2的圆 分别在半平面
分别在半平面 、
、 内,且与棱
内,且与棱 切于同一点P,则以圆
切于同一点P,则以圆
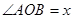 ,当直
,当直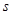 关于
关于 的函数
的函数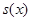 =____________________.
=____________________.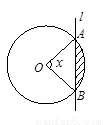
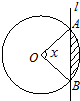 如图,半径为1的圆与直线l相交于A、B两个不同的点,设∠AOB=x,当直线l平行移动时,则圆被直线扫过部分(图中阴影部分)的面积s关于x的函数s(x)=________.
如图,半径为1的圆与直线l相交于A、B两个不同的点,设∠AOB=x,当直线l平行移动时,则圆被直线扫过部分(图中阴影部分)的面积s关于x的函数s(x)=________.