Question

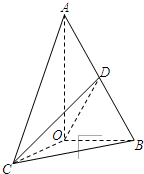
如图，已知△AOB的一个顶点为抛物线y²=2x的顶点O，A、B两点都在抛物线上，且∠AOB=90°．
（1）证明直线AB必过一定点；
（2）求△AOB面积的最小值．

Answer 1

证明：（1）设OA所在直线的方程为y=kx（k≠0），则直线OB的方程为y=-

1

k

x，
由

y=kx y2=2x

解得

x=0 y=0

或

x= 2 k2 y= 2 k

即A点的坐标为（

2

k2

，

2

k

）．
同样由

y=- 1 k x y2=2x

解得B点的坐标为（2k²，-2k）．
∴AB所在直线的方程为y+2k=

2 k +2k

2 k2 -2k2

（x-2k²），
化简并整理，得（

1

k

-k）y=x-2．
不论实数k取任何不等于0的实数，当x=2时，恒有y=0．
故直线过定点P（2，0）．
（2）解　由于AB所在直线过定点P（2，0），所以可设AB所在直线的方程为x=my+2．
由

x=my+2 y2=2x

消去x并整理得y²-2my-4=0．
∴y₁+y₂=2m，y₁y₂=-4．
于是|y₁-y₂|=

(y1-y2)2

=

(y1+y2)2-4y1y2

=

(2m)2+16

=2

m2+4

．
S_△AOB=

1

2

×|OP|×（|y₁|+|y₂|）
=

1

2

|OP|•|y₁-y₂|=

1

2

×2×2

m2+4

=2

m2+4

．
∴当m=0时，△AOB的面积取得最小值为4．