题目内容
甲、乙两人进行一项游戏比赛,比赛规则如下:甲从区间[0,1]上随机等可能地抽取一个实数记为b,乙从区间[0,1]上随机等可能地抽取一个实数记为c(b,c可以相等),若关于x的方程x2+2bx+c=0有实根,则甲获胜,否则乙获胜.(Ⅰ)求一场比赛中甲获胜的概率;
(Ⅱ)设n场比赛中,甲恰好获胜k场的概率为Pnk(k≤n,k∈N,n∈N*),求
| n |
 |
| k=0 |
| k |
| n |
| P | k n |
分析:(1)由题意知本题是一个几何概型,试验发生包含的事件是边长为1的正方形的面积,满足条件的事件是方程x2+2bx+c=0有实根的充要条件,写出变量满足的关系式,用积分求出面积,做比值得到结果.
(2)由题意知本题符合独立重复试验的条件,根据独立重复试验的公式写出概率,表示出和式,问题转换为二项式定理的应用,根据组合数把式子变形,提出公因式,逆用二项式定理,得到结果.
(2)由题意知本题符合独立重复试验的条件,根据独立重复试验的公式写出概率,表示出和式,问题转换为二项式定理的应用,根据组合数把式子变形,提出公因式,逆用二项式定理,得到结果.
解答:解:(1)由题意知本题是一个几何概型,
试验发生包含的事件是边长为1的正方形的面积,
满足条件的事件是方程x2+2bx+c=0有实根的充要条件是△=4b2-4c≥0,即b2≥c
由题意知,每场比赛中甲获胜的概率为P1=
=
b3|01=
(2)∵由题意知本题符合独立重复检验的条件,
∴n场比赛中甲恰好获胜k场的概率为Pnk=
(
)k(
)n-k
∴
=
(
)0 (
)n+
(
)1(
)n-1+…+
(
)r(
)n-r+…+
(
)n
又
=
•
=Cn-1r-1,
∴
=
(
)1(
)n-1+
(
)2(
)n-2+…+
(
)n(
)0
=
[
(
)0(
)n-1+
(
)1(
)n-2+…
(
)n-1(
)0]
=
(
+
)n-1=
试验发生包含的事件是边长为1的正方形的面积,
满足条件的事件是方程x2+2bx+c=0有实根的充要条件是△=4b2-4c≥0,即b2≥c
由题意知,每场比赛中甲获胜的概率为P1=
| ||
| 1 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)∵由题意知本题符合独立重复检验的条件,
∴n场比赛中甲恰好获胜k场的概率为Pnk=
| C | k n |
| 1 |
| 3 |
| 2 |
| 3 |
∴
| n |
 |
| k=0 |
| k |
| n |
| P | k n |
| C | 0 n |
| 0 |
| n |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 1 n |
| 1 |
| n |
| 1 |
| 3 |
| 2 |
| 3 |
| C | r n |
| r |
| n |
| 1 |
| 3 |
| 2 |
| 3 |
| C | n n |
| n |
| n |
| 1 |
| 3 |
又
| C | r n |
| r |
| n |
| n! |
| r!(n-r)! |
| r |
| n |
∴
| n |
 |
| k=0 |
| k |
| n |
| P | k n |
| C | 0 n-1 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 1 n-1 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | n-1 n-1 |
| 1 |
| 3 |
| 2 |
| 3 |
=
| 1 |
| 3 |
| C | 0 n |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 1 n-1 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | n-1 n-1 |
| 1 |
| 3 |
| 2 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
点评:这是一个中档题,培养运用从具体到抽象、从特殊到一般的分析问题的能力,充分体现数学的化归思想.启发诱导的同时,训练了学生观察和概括归纳的能力.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
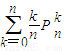 的值.
的值.