Question

已知双曲线的左，右焦点分别为，点P在双曲线的右支上，且，求此双曲线的离心率e的最大值．

Answer 1

解析:

【解题思路】这是一个存在性问题，可转化为最值问题来解决。

 (方法1)由定义知，又已知，解得，，在中，由余弦定理，得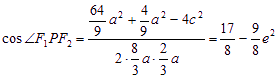，要求的最大值，即求的最小值，当时，解得．即的最大值为．

(方法2)  ，

双曲线上存在一点P使，等价于

 (方法3)设，由焦半径公式得，∵，∴，∴，∵，∴，∴的最大值为．

【名师指引】（1）解法1用余弦定理转化，解法2用定义转化，解法3用焦半径转化；

（2）点P在变化过程中，的范围变化值得探究；

（3）运用不等式知识转化为的齐次式是关键