题目内容
已知f(x)=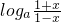 ,(a>0,且a≠1).
,(a>0,且a≠1).
(1)求f(x)的定义域.
(2)证明f(x)为奇函数.
(3)求使f(x)>0成立的x的取值范围.
解:(1)f(x)=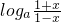 ,(a>0,且a≠1)的定义域为:{x|
,(a>0,且a≠1)的定义域为:{x|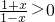 },
},
解得f(x)=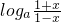 ,(a>0,且a≠1)的定义域为{x|-1<x<1}.
,(a>0,且a≠1)的定义域为{x|-1<x<1}.
(2)∵f(x)=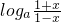 ,(a>0,且a≠1),
,(a>0,且a≠1),
∴f(-x)= =-
=-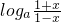 =-f(x),
=-f(x),
∴f(x)为奇函数.
(3)∵f(x)=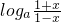 ,(a>0,且a≠1),
,(a>0,且a≠1),
∴由f(x)>0,得 ,
,
当0<a<1时,有0< <1,解得-1<x<0;
<1,解得-1<x<0;
当a>1时,有 >1,解得0<x<1;
>1,解得0<x<1;
∴当a>1时,使f(x)>0成立的x的取值范围是(0,1),
当0<a<1时,使f(x)>0成立的x的取值范围是(-1,0).
分析:(1)f(x)=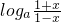 ,(a>0,且a≠1)的定义域为:{x|
,(a>0,且a≠1)的定义域为:{x|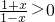 },由此能求出结果.
},由此能求出结果.
(2)由f(x)=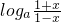 ,(a>0,且a≠1),知f(-x)=
,(a>0,且a≠1),知f(-x)= =-
=-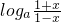 =-f(x),由此能证明f(x)为奇函数.
=-f(x),由此能证明f(x)为奇函数.
(3)由f(x)>0,得 ,对a分类讨论可得关于x的方程,由此能求出使f(x)>0成立的x的取值范围.
,对a分类讨论可得关于x的方程,由此能求出使f(x)>0成立的x的取值范围.
点评:本题考查f(x)的定义域的求法,证明f(x)为奇函数,求使f(x)>0成立的x的取值范围,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
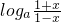 ,(a>0,且a≠1)的定义域为:{x|
,(a>0,且a≠1)的定义域为:{x|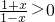 },
},解得f(x)=
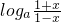 ,(a>0,且a≠1)的定义域为{x|-1<x<1}.
,(a>0,且a≠1)的定义域为{x|-1<x<1}.(2)∵f(x)=
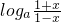 ,(a>0,且a≠1),
,(a>0,且a≠1),∴f(-x)=
 =-
=-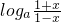 =-f(x),
=-f(x),∴f(x)为奇函数.
(3)∵f(x)=
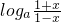 ,(a>0,且a≠1),
,(a>0,且a≠1),∴由f(x)>0,得
 ,
,当0<a<1时,有0<
 <1,解得-1<x<0;
<1,解得-1<x<0;当a>1时,有
 >1,解得0<x<1;
>1,解得0<x<1;∴当a>1时,使f(x)>0成立的x的取值范围是(0,1),
当0<a<1时,使f(x)>0成立的x的取值范围是(-1,0).
分析:(1)f(x)=
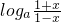 ,(a>0,且a≠1)的定义域为:{x|
,(a>0,且a≠1)的定义域为:{x|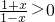 },由此能求出结果.
},由此能求出结果.(2)由f(x)=
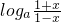 ,(a>0,且a≠1),知f(-x)=
,(a>0,且a≠1),知f(-x)= =-
=-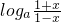 =-f(x),由此能证明f(x)为奇函数.
=-f(x),由此能证明f(x)为奇函数.(3)由f(x)>0,得
 ,对a分类讨论可得关于x的方程,由此能求出使f(x)>0成立的x的取值范围.
,对a分类讨论可得关于x的方程,由此能求出使f(x)>0成立的x的取值范围.点评:本题考查f(x)的定义域的求法,证明f(x)为奇函数,求使f(x)>0成立的x的取值范围,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x)=e3ax-3ax(a≠0),则
的值为( )
| lim |
| x→0 |
| f′(x) |
| eax-1 |
| A、a | B、2a | C、3a | D、9a |
已知f(x)=alnx+
x2(a>0),若对任意两个不等的正实数x1,x2,都有
>2恒成立,则a的取值范围是( )
| 1 |
| 2 |
| f(x1)-f(x2) |
| x1-x2 |
| A、(0,1] |
| B、(1,+∞) |
| C、(0,1) |
| D、[1,+∞) |