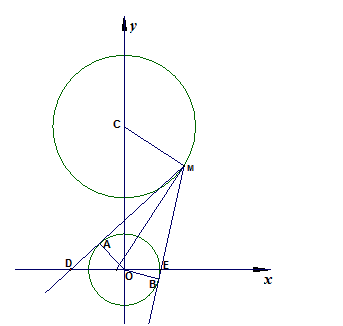题目内容
设M点是圆C:x2+(y-4)2=4上的动点,过点M作圆O:x2+y2=1的两条切线,切点分别为A,B,切线MA,MB分别交x轴于D,E两点.是否存在点M,使得线段DE被圆C在点M处的切线平分?若存在,求出点M的纵坐标;若不存在,说明理由.
分析:设存在点M(x0,y0)满足条件,设过点M且与圆O相切的直线方程为:y-y0=k(x-x0)通过点到直线的距离公式,求出直线MA,MB的斜率分别为k1,k2的关系,通过圆C在点M处的切线方程,求出切线与x轴的交点坐标,D,E的坐标,然后利用斜率关系式求出点M的纵坐标.
解答:解:设存在点M(x0,y0)满足条件
设过点M且与圆O相切的直线方程为:y-y0=k(x-x0)
则由题意得,
=1,化简得:(x02-1)k2-2x0y0k+y02-1=0
设直线MA,MB的斜率分别为k1,k2,则k1+k2=
,k1k2=
圆C在点M处的切线方程为y-y0=
(x-x0)
令y=0,得切线与x轴的交点坐标为(
+x0,0)
又得D,E的坐标分别为(
+x0,0),(
+x0,0)
由题意知,2(
+x0)=
+x0+
+x0
用韦达定理代入可得,
=
,与x02+(y0-4)2=4联立,
得y0=
设过点M且与圆O相切的直线方程为:y-y0=k(x-x0)
则由题意得,
| |-kx0+y0| | ||
|
设直线MA,MB的斜率分别为k1,k2,则k1+k2=
| 2x0y0 |
| x02-1 |
| y02-1 |
| x02-1 |
圆C在点M处的切线方程为y-y0=
| -x0 |
| y0-4 |
令y=0,得切线与x轴的交点坐标为(
| y02-4y0 |
| x0 |
又得D,E的坐标分别为(
| -y0 |
| k1 |
| -y0 |
| k2 |
由题意知,2(
| y02-4y0 |
| x0 |
| -y0 |
| k1 |
| -y0 |
| k2 |
用韦达定理代入可得,
| y 0-4 |
| x0 |
| -x0y0 |
| y02-1 |
得y0=
13+
| ||
| 8 |
点评:本题考查直线与圆的位置关系,点到直线的距离公式的应用,圆的切线方程的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目