题目内容
已知函数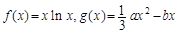 ,其中a,b∈R
,其中a,b∈R
(1)求函数f(x)的最小值;
(2)当a>0,且a为常数时,若函数h(x)=x[g(x)+1]对任意的x1>x2≥4,总有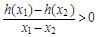 成立,试用a表示出b的取值范围;
成立,试用a表示出b的取值范围;
(3)当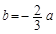 时,若
时,若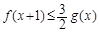 对x∈[0,+∞)恒成立,求a的最小值.
对x∈[0,+∞)恒成立,求a的最小值.
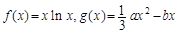 ,其中a,b∈R
,其中a,b∈R(1)求函数f(x)的最小值;
(2)当a>0,且a为常数时,若函数h(x)=x[g(x)+1]对任意的x1>x2≥4,总有
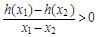 成立,试用a表示出b的取值范围;
成立,试用a表示出b的取值范围;(3)当
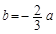 时,若
时,若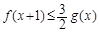 对x∈[0,+∞)恒成立,求a的最小值.
对x∈[0,+∞)恒成立,求a的最小值.(1) ;(2)
;(2) 时,
时, ,
, 时,
时, ;(3)1
;(3)1
 ;(2)
;(2) 时,
时, ,
, 时,
时, ;(3)1
;(3)1试题分析:(1)利用导数判断出函数
 的单调性,即可求出
的单调性,即可求出 的最小值;(2)解决本题的关键是由“对任意的x1>x2≥4,总有
的最小值;(2)解决本题的关键是由“对任意的x1>x2≥4,总有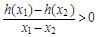 成立”得出“
成立”得出“ 在
在 上单调递增”,从而再次转化为导函数大于0的问题求解;(3)通过构造函数
上单调递增”,从而再次转化为导函数大于0的问题求解;(3)通过构造函数 ,转化为
,转化为 对
对 恒成立,于是转化为求
恒成立,于是转化为求 在
在 上的最大值问题求解.解题过程中要注意对参数的合理分类讨论.
上的最大值问题求解.解题过程中要注意对参数的合理分类讨论.试题解析:(1)∵
 ,令
,令 ,得
,得
∴
 在(0,
在(0, )上单调递减,在(
)上单调递减,在( ,+∞)上单调递增
,+∞)上单调递增∴
 在
在 处取得最小值
处取得最小值即
 ; 4分
; 4分(2)由题意,得
 在
在 上单调递增
上单调递增∴
 在
在 上恒成立
上恒成立∴
 在
在 上恒成立 5分
上恒成立 5分构造函数

则

∴F(x)在
 上单调递减,在
上单调递减,在 上单调递增
上单调递增(i)当
 ,即
,即 时,F(x)在
时,F(x)在 上单调递减,在
上单调递减,在 上单调递增
上单调递增∴

∴
 ,从而
,从而 7分
7分(ii)当
 ,即
,即 时,F(x)在(4,+∞)上单调递增
时,F(x)在(4,+∞)上单调递增 ,从而
,从而 8分
8分综上,当
 时,
时, ,
, 时,
时, ; 9分
; 9分(3)当
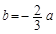 时,构造函数
时,构造函数
由题意,有
 对
对 恒成立
恒成立∵

(i)当
 时,
时,
∴
 在
在 上单调递增
上单调递增∴
 在
在 上成立,与题意矛盾. 11分
上成立,与题意矛盾. 11分(ii)当
 时,令
时,令
则
 ,由于
,由于
①当
 时,
时, ,
, 在
在 上单调递减
上单调递减∴
 ,即
,即 在
在 上成立
上成立∴
 在
在 上单调递减
上单调递减∴
 在
在 上成立,符合题意 12分
上成立,符合题意 12分②当
 时,
时,
∴
 在
在 上单调递增,在
上单调递增,在 上单调递减
上单调递减∵

∴
 在
在 成立,即
成立,即 在
在 成立
成立∴
 在
在 上单调递增
上单调递增∴
 在
在 上成立,与题意矛盾 13分
上成立,与题意矛盾 13分综上,a的最小值为1 14分

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
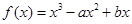 的图象为曲线E.
的图象为曲线E.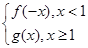 ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由. 在
在 处的切线
处的切线 ,则
,则 的导函数
的导函数 的图像如图所示,那么
的图像如图所示,那么

 在
在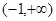 上是减函数,则
上是减函数,则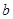 的取值范围是( )
的取值范围是( )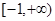
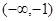
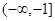
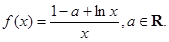 .则有
.则有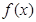 的极大值为________.
的极大值为________. 的首项为
的首项为 ,且
,且 ,则数列
,则数列
