题目内容
已知A(2,3)、B(-1,5)且满足
解析一:设C(x1,y1),D(x2,y2),E(x3,y3),
∵![]() =(x1-2,y1-3),
=(x1-2,y1-3), ![]() =(-3,2),
=(-3,2),
∴![]() =(x2-2,y2-3),
=(x2-2,y2-3),
![]() =(x3-2,y3-3).
=(x3-2,y3-3).
由条件得(x1-2,y1-2)=![]() (-3,2),
(-3,2),
(x2-2,y2-3)=3(-3,2),(x3-2,y3-3)=-![]() (-3,2).
(-3,2).
从而
∴C(1,![]() ),D(-7,9),E(
),D(-7,9),E(![]() ,
,![]() ).
).
解析二:由![]() =3
=3![]() =3(
=3(![]() +
+![]() ),得
),得![]() =-
=-![]()
![]() .
.
由![]() =-
=-![]() (
(![]() +
+![]() ),得
),得![]() =-
=-![]()
![]() .
.
由![]() =
=![]()
![]() =
=![]() (
(![]() +
+![]() ),得
),得![]() =
=![]()
![]() .
.
由定比分点公式,可得x1=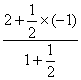 =1,
=1,
y1=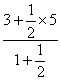 =
=![]() ;
;
x2=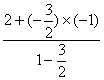 =-7,
=-7,
y2=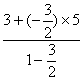 =9;
=9;
x3=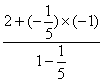 =
=![]() ,y3=
,y3=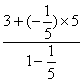 =
=![]() .
.
∴C(1,![]() ),D(-7,9),E(
),D(-7,9),E(![]() ,
,![]() ).
).
点评:本题是向量坐标表示的典型题,解析一主要是运用若向量相等,则其坐标相等这一原理来解,思路清晰,易于理解.解析二主要运用定比分点公式求点的坐标,此题关键在于求λ,将已知向量关系进行分解达到![]() =λ
=λ![]() ,
,![]() =λ
=λ![]() ,
,![]() =λ
=λ![]() 的形式,从而分别求出λ.
的形式,从而分别求出λ.

练习册系列答案
相关题目