题目内容
在△ABC中,若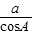 =
=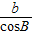 =
=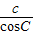 ,则△ABC是( )
,则△ABC是( )A.直角三角形
B.等边三角形
C.钝角三角形
D.等腰直角三角形
【答案】分析:先根据正弦定理将边的关系变为角的关系,进而再由两角和与差的正弦公式确定B=C得到三角形是等腰三角形.
解答:解:由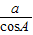 =
=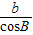 ,得
,得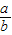 =
=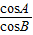 .
.
又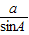 =
=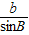 ,∴
,∴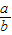 =
=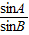 .
.
∴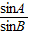 =
=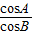 .∴sinAcosB=cosAsinB,
.∴sinAcosB=cosAsinB,
sin(A-B)=0,A=B.同理B=C.
∴△ABC是等边三角形.
故选B.
点评:本题主要考查正弦定理和两角和与差的正弦公式的应用.三角函数公式比较多,要对公式强化记忆.
解答:解:由
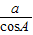 =
=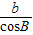 ,得
,得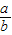 =
=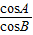 .
.又
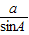 =
=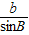 ,∴
,∴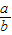 =
=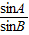 .
.∴
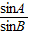 =
=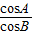 .∴sinAcosB=cosAsinB,
.∴sinAcosB=cosAsinB,sin(A-B)=0,A=B.同理B=C.
∴△ABC是等边三角形.
故选B.
点评:本题主要考查正弦定理和两角和与差的正弦公式的应用.三角函数公式比较多,要对公式强化记忆.

练习册系列答案
相关题目
在△ABC中,若acosA=bcosB,则△ABC的形状是( )
| A、等腰三角形 | B、直角三角形 | C、等腰直角三角形 | D、等腰或直角三角形 |
在△ABC中,若sinB=
,cosC=
,则cosA的值是( )
| 4 |
| 5 |
| 12 |
| 13 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|