题目内容
17.向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{1}{2}$,<$\overrightarrow{a}$-$\overrightarrow{c}$,$\overrightarrow{b}$-$\overrightarrow{c}$>=60°,则|$\overrightarrow{c}$|的最大值为2.分析 根据题意,求出$\overrightarrow{a}$、$\overrightarrow{b}$夹角的大小,画出图形表示$\overrightarrow{a}$-$\overrightarrow{c}$、$\overrightarrow{b}$-$\overrightarrow{c}$与$\overrightarrow{b}$-$\overrightarrow{a}$,
求出|$\overrightarrow{b}$-$\overrightarrow{a}$|的值,再根据正弦定理求出三角形外接圆的直径,即为OC的最大值.
解答 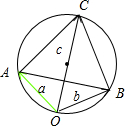 解:∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,
解:∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|×|$\overrightarrow{b}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=-$\frac{1}{2}$,
∴<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{2π}{3}$,
如图所示:
设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,
则$\overrightarrow{CA}$=$\overrightarrow{a}$-$\overrightarrow{c}$,$\overrightarrow{CB}$=$\overrightarrow{b}$-$\overrightarrow{c}$,
∴$\overrightarrow{AB}$=$\overrightarrow{b}$-$\overrightarrow{a}$,
${\overrightarrow{AB}}^{2}$=${\overrightarrow{b}}^{2}$+${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}$•$\overrightarrow{b}$=1+1-2×(-$\frac{1}{2}$)=3,
∴|$\overrightarrow{AB}$|=$\sqrt{3}$,
由正弦定理得:
△OAB的外接圆直径为
2R=$\frac{AB}{sin∠ACB}$=$\frac{\sqrt{3}}{sin\frac{2π}{3}}$=2,
∴当OC为直径时,它的模最大,最大值为2,
故答案为:2.
点评 本题考查了平面向量的应用问题,也考查了四点共圆的应用问题以及正弦定理的应用问题,是综合性题目.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | (1,+∞) | B. | ($\frac{2\sqrt{3}}{3}$,+∞) | C. | ($\frac{\sqrt{5}+1}{2}$,+∞) | D. | ($\sqrt{2}$+1,+∞) |
| A. | $\frac{3}{20}$ | B. | $\frac{3}{16}$ | C. | $\frac{7}{20}$ | D. | $\frac{2}{5}$ |
| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$+1 | C. | $\sqrt{3}$-1 | D. | $\sqrt{3}$+1 |
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
 如图所示:在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,O,Q分别为AB,PA的中点,G为△AOC的重心,AC=$\sqrt{3}$,∠ABC=30°
如图所示:在三棱锥P-ABC中,PA⊥底面ABC,AC⊥BC,O,Q分别为AB,PA的中点,G为△AOC的重心,AC=$\sqrt{3}$,∠ABC=30°