题目内容
设O是正△ABC的中心，则向量
、
、
是（ ）
| AO |
| OB |
| OC |
| A、有相同起点的向量 |
| B、平行向量 |
| C、模相等的向量 |
| D、相等向量 |
分析：根据正三角形的中心到三个顶点的距离相等，得到这三个向量的模长相等，而这三个向量的方向不同，起点不同，所以它们只有模长相等一个条件成立．
解答：解：∵O是正△ABC的中心，
∴向量
、
、
分别是以三角形的顶点和中心为起点和终点的，
∵O是正三角形的中心，
∴O到三个顶点的距离相等，
即|
|=|
|=|
|，
故选C．
∴向量
| AO |
| OB |
| OC |
∵O是正三角形的中心，
∴O到三个顶点的距离相等，
即|
| AO |
| OB |
| OC |
故选C．
点评：不同考查向量的模，考查向量的几何表示，考查正三角形的中心点特点，题目中涉及到多个向量的基本概念，是一个基础题．
练习册系列答案
初中暑期衔接系列答案
相关题目
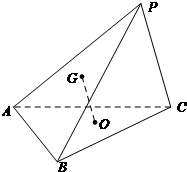如图，在三棱锥P-ABC中，△ABC是正三角形，且∠PCA=∠PCB．
用向量探索几何的性质：
如图，在正四棱锥S-ABCD中，AB=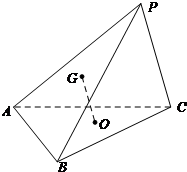
如图，在三棱锥P-ABC中，△ABC是正三角形，且∠PCA=∠PCB．