题目内容
已知圆 ,直线
,直线 过定点A(1,0)
过定点A(1,0)
(1)若直线 平分圆的周长,求直线
平分圆的周长,求直线 的方程;
的方程;
(2)若直线 与圆相切,求直线
与圆相切,求直线 的方程;
的方程;
(3)若直线 与圆C交于PQ两点,求△CPQ面积的最大值,并求此时的直线方程.
与圆C交于PQ两点,求△CPQ面积的最大值,并求此时的直线方程.
2x-y-2=0, 或
或 ,面积最大值为
,面积最大值为 y=x-1或y=7x-7
y=x-1或y=7x-7
【解析】(1)因为直线 平分圆的周长,所以直线过圆心(2,2),又因为直线
平分圆的周长,所以直线过圆心(2,2),又因为直线 过定点A(1,0),2所以直线的斜率为
过定点A(1,0),2所以直线的斜率为 ,所以直线方程为2x-y-2=0 3
,所以直线方程为2x-y-2=0 3
(2)直线 过定点A(1,0),设直线方程为
过定点A(1,0),设直线方程为 ,因为直线与圆相切,所以圆心到直线的距离等于半径
,因为直线与圆相切,所以圆心到直线的距离等于半径 ,解得
,解得 ,直线方程为
,直线方程为
因为过圆外一点能做两条切线,所以另外一条斜率不存在,所以直线方程为
所以切线方程为 或
或 (漏x=1扣2分) 9
(漏x=1扣2分) 9
(3) 11
11
“=”成立时,角PCQ=90°,∴ 13
13
由题意,直线l斜率存在,∴设l方程为y=k(x-1)解得k=1或7,
∴所求方程为y=x-1或y=7x-7 16
考点:本题考查直线与圆的位置关系

练习册系列答案
相关题目
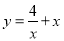 的最大值是 ( )
的最大值是 ( )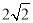 B.4 C.-4 D.-
B.4 C.-4 D.- 的单调增区间是 .
的单调增区间是 . 没有实根,则
没有实根,则 的取值范围是 .
的取值范围是 . 的离心率e=
的离心率e= ,A,B是椭圆的左右顶点,P为椭圆上不同于AB的动点,直线PA,PB的倾斜角分别为
,A,B是椭圆的左右顶点,P为椭圆上不同于AB的动点,直线PA,PB的倾斜角分别为 ,则
,则 = .
= . 的左顶点为圆心,且与双曲线的渐近线相切的圆的方程为
的左顶点为圆心,且与双曲线的渐近线相切的圆的方程为  ,
, ,则向量
,则向量 在向量
在向量 方向上的投影是 .
方向上的投影是 .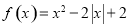 的定义域是
的定义域是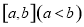 ,值域是
,值域是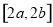 ,则符合条件的数组
,则符合条件的数组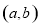 的组数为( )
的组数为( )