题目内容
在某次1(1)3人都通过体能测试的概率;
(2)只有2人通过体能测试的概率;
(3)只有1人通过体能测试的概率.
解:设A表示事件“甲通过体能测试”,B表示事件“乙通过体能测试”,C表示事件“丙通过体能测试”.由题意有 P(A)= (1)设M1表示“甲、乙、丙3人都通过体能测试”,即M1=ABC.由事件A、B、C相互独立,可得 P(M1)=P(A)P(B)P(C)= (2)设M2表示事件“甲、乙、丙3人只有2人通过体能测试”,则 M2=AB 由于事件A、B、 P(M2)=P(A)P(B)P( (3)设M3表示事件“甲、乙、丙3人只有1人通过体能测试”,则 M3=A 由于A、 P(M3)=P(A)P(![]() ,P(B)=
,P(B)=![]() ,P(C)=
,P(C)= ![]() .
.![]() .
.![]() +
+![]() BC+
BC+![]() C.
C.![]() ,A、
,A、![]() 、C,
、C,![]() 、B、C均相互独立,并且事件AB
、B、C均相互独立,并且事件AB![]() 、A
、A![]() C、
C、![]() BC两两互斥,因此所求的概率为
BC两两互斥,因此所求的概率为![]() )+P(A)P(
)+P(A)P(![]() )P(C)+P(
)P(C)+P(![]() )P(B)P(C)=
)P(B)P(C)=![]() .
.![]() +
+![]() B
B![]() +
+![]()
![]() C.
C.![]() 、
、![]() ,
,![]() 、B、
、B、![]() ,
,![]() 、
、![]() 、C相互独立,并且事件A
、C相互独立,并且事件A![]()
![]() ,
,![]() B
B![]() ,
,![]() ?
?![]() C两两互斥,所以所求的概率为
C两两互斥,所以所求的概率为![]() )P(
)P(![]() )+P(
)+P(![]() )P(B)P(
)P(B)P(![]() )+P(
)+P(![]() )P(
)P(![]() )P(C)=
)P(C)=![]() .
.
掌控中考系列答案
68所名校图书毕业升学全真模拟试卷系列答案
国华图书中考拐点系列答案
创新能力学习中考总复习系列答案
核按钮系列答案
高效复习新疆中考系列答案
高中总复习优化设计系列答案
六大名校中考冲刺卷系列答案
荣德基点拨中考系列答案
上海名师导学系列答案
 2008年北京奥运会中国跳水梦之队取得了辉煌的成绩.据科学测算,跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动轨迹(如图所示)是一经过坐标原点的抛物线(图中标出数字为已知条件),且在跳某个规定动作时,正常情况下运动员在空中的最高点距水面
2008年北京奥运会中国跳水梦之队取得了辉煌的成绩.据科学测算,跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动轨迹(如图所示)是一经过坐标原点的抛物线(图中标出数字为已知条件),且在跳某个规定动作时,正常情况下运动员在空中的最高点距水面 2008年北京奥运会中国跳水梦之队取得了辉煌的成绩.据科学测算,跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动轨迹(如图所示)是一经过坐标原点的抛物线(图中标出数字为已知条件),且在跳某个规定动作时,正常情况下运动员在空中的最高点距水面
2008年北京奥运会中国跳水梦之队取得了辉煌的成绩.据科学测算,跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动轨迹(如图所示)是一经过坐标原点的抛物线(图中标出数字为已知条件),且在跳某个规定动作时,正常情况下运动员在空中的最高点距水面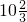 米,入水处距池边4米,同时运动员在距水面5米或5米以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
米,入水处距池边4米,同时运动员在距水面5米或5米以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误. 米,问此次跳水会不会失误?请通过计算说明理由;
米,问此次跳水会不会失误?请通过计算说明理由; 米,入水处距池边4米,同时运动员在距水面5米或5米以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
米,入水处距池边4米,同时运动员在距水面5米或5米以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误. 米,问此次跳水会不会失误?请通过计算说明理由;
米,问此次跳水会不会失误?请通过计算说明理由;
 米,入水处距池边4米,同时运动员在距水面5米或5米以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
米,入水处距池边4米,同时运动员在距水面5米或5米以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误. 米,问此次跳水会不会失误?请通过计算说明理由;
米,问此次跳水会不会失误?请通过计算说明理由;